Cet article rassemble quelques éléments concernant le chapitre d’arithmétique et nombres premiers du cours de troisième de collège conforme aux nouveaux programmes de mathématiques du collège de 2016.
Le nouveau programme 2016 cycle 4 en mathématiques
Activités : le jeu de Juniper-Green
Activité : le crible d’Erathostène
Activité : une énigme sur le engrenages
—
Le nouveau programme 2016 cycle 4 en mathématiques
Voici un extrait des nouveaux programmes de collèges en mathématiques (BO du 17 juillet 2018 modifiant les programmes de 2015) concernant la partie arithmétique et nombres premiers
Comprendre et utiliser les notions de divisibilité et de nombres premiers
|
CONNAISSANCES
Multiples et diviseurs Critères de divisibilité par 2, 3, 5, 9 Division euclidienne (quotient, reste) Définition d’un nombre premier Liste des nombres premiers inférieurs ou égaux à 30 Fractions irréductibles. |
COMPÉTENCES ASSOCIÉES
Déterminer si un entier est ou n’est pas multiple ou diviseur d’un autre entier Déterminer les nombres premiers inférieurs ou égaux à 100 Utiliser les critères de divisibilité par 2, 3, 5, 9, 10 Déterminer les diviseurs d’un nombre à la main, à l’aide d’un tableur, d’une calculatrice Décomposer un nombre entier en produit de facteurs premiers (à la main ou à l’aide d’un logiciel) Simplifier une fraction pour la rendre irréductible Modéliser et résoudre des problèmes mettant en jeu la divisibilité (engrenages, conjonction de phénomènes, etc.) |
Activités
Le jeu de Juniper Green
Ce jeu mathématique à deux joueurs a été crée par Richard Porteous à l’école de Juniper Green. Il permet de travailler les notions de multiples, diviseurs et nombres premiers pour établir une stratégie gagnante. Ian Stewart, célèbre mathématicien anglais, grand vulgarisateur des mathématiques dans le mensuel Pour la science a détaillé ce jeu dans le numéro 237 de juillet 1992.
Voici un lien où vous trouverez cet article dans sa version anglaise du Scientific American.
Je vous propose ci-dessous plusieurs versions de ce jeux à utiliser en classe.
Version 40 à 3 règles
|
Jouez à deux à ce jeu et essayez de déterminer la stratégie gagnante.
Version 40 à 4 règles
On peut compliquer la stratégie gagnante en imposant une dernière règle :
|
Jouez à deux à ce jeu et essayez de déterminer la stratégie gagnante.
Version 40 à 4 règles : le défi
|
À deux en partenariat essayez de trouver la plus longue suite de nombres correspondant à une partie de Juniper Green.
Quelques pistes et extensions
Ce jeu permet de faire apparaître la notion de nombre premier.
Voici une partie avec le jeu à 3 règles : 35 – 7 – 21 – 3 – 30 – 10 – 5 – 25 – 1 – 23
Quand un joueur choisi le nombre 1, le choix d’un nombre premier supérieur à la moitié de 40 assure la victoire.
Si le premier joueur choisi un nombre premier, il gagne en obligeant le second à passer par le nombre 1 d’où la mise ne place de la règle 4.
Voici une partie avec le jeu à 4 règles : 18 – 36 – 9 – 27 – 3 – 24 – 8 – 40 – 10 – 20 – 4 – 12 – 6 – 2 – 32 – 16 – 1 – 31
Cette partie volontairement plus longue illustre bien la complexité de ce jeu.
La recherche de la plus longue suite de nombres correspondant à une partie est vraiment intéressante. L’exemple précédent contient 18 nombres, on peut certainement faire mieux.
Par exemple : 40 – 20 – 10 – 30 – 15 – 5 – 35 – 7 – 21 – 3 – 6 – 12 – 24 – 4 – 8 – 16 – 32 – 2 – 14 – 28 – 1 – 9 – 18 – 36 soit 24 nombres. Mais on doit pouvoir faire mieux ?!!
Un de mes élèves vient de trouver 27 nombres : 22 -11 – 33 – 1 – 16 – 32 – 8 – 24 – 12 – 36 – 9 – 18 – 6 – 3 – 21 – 7 – 35 – 5 – 10 – 20 – 40 – 4 – 28 – 14 – 2 – 38 – 19
D’après l’article de Ian Stewart cité ci dessus, il n’existe pas à ce jour de réponse générale à cette dernière question quand on modifie la borne supérieure (Nmax=40 dans cet article )
On peut faire réfléchir nos élèves sur le même jeu avec une borne supérieure de 100.
Vous trouverez en suivant ce lien une version en ligne du jeu qui permet de tester le mode défi.
Enfin je signale que le numéro 427 du bulletin vert de l’APMEP de 2000 contient un article sur ce sujet, mais j’ai tous les numéros à la maison depuis le …. 430….
Le crible d’Erathostène
C’est une méthode pour déterminer une liste de nombres premiers inférieurs à une borne fixé à l’avance.
Elle illustre la thématique de ce chapitre sur l’arithmétique et les nombres premiers.
Brièvement, cet algorithme consiste à constituer une liste d’entier. On commence ensuite à entourer le premier nombre premier : 2. On supprime ensuite tous les multiples de 2 en les rayant dans le tableau. On reprend alors le tableau au début et on cherche la première case non cochée, il s’agit du 3. On raye les multiples de 3 qui subsiste dans le tableau… et ainsi de suite. Pour information, un crible est au départ un tamis qui permet de filtrer les solides suivant leur taille, par exemple pour trier les pommes de terre en agriculture. Le crible d’Erathostène permet de trier les nombres pour ne garder que les premiers !

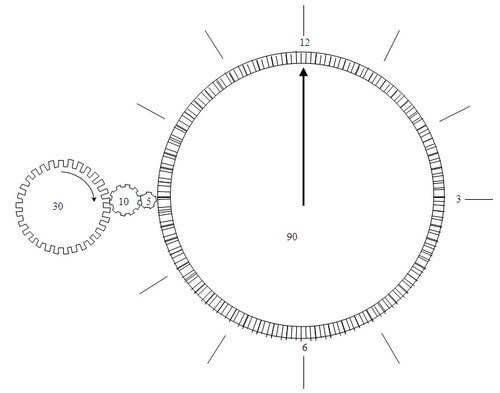
Une énigme sur les engrenages
Le mécanisme décrit ci-dessus est constitué de quatre engrenages dont le nombre de dents est indiqué au centre de chacun. 30 dents pour le premier, 10 pour le second, 5 pour le troisième et 90 pour le dernier.
Dans le plus grand engrenage se trouve une aiguille qui tourne avec l’engrenage. Cette aiguille pointe au départ vers le 12 et pointera ensuite vers des nombres différents.
Sur quel nombre pointera cette aiguille quand le premier engrenage aura fait un tour complet ?
Voici la fiche en pdf que je distribue en classe.
Cette énigme prépare le travail suivant sur le braquet. Elle illustre aussi le fait que deux engrenages successifs tournent dans des sens différents et que la parité du nombre d’engrenages permet de connaître le sens. Il introduit la notion de braquet.
Les braquets d’un vélo
Une vidéo pour clarifier le fonctionnement du vélo. On y voit le plateau avant, la cassette arrière avec les pignons, la chaine…
https://www.youtube.com/watch?v=0qscPqOHPyE
Voici une première partie de cette activité qui consiste à étudier un dérailleur simple constitué d’un grand plateau à l’avant et de 3 pignons à l’arrière. Il s’agit de définir la notion de braquet et de développement. L’exemple est construit de telle manière que le classement des braquets ne soit pas le classement intuitif habituel. En effet pour changer les vitesses suivant les braquets croissant cela demande un peu de mathématiques !

Je vous propose également en suivant une activité semblable pour le tableur. On étudie cette fois-ci un vélo à 24 vitesses, ce qui nécessite d’utiliser les capacités de calculs du tableur.

Le plan du cours
- La division euclidienne
- Diviseur, multiple et critères de divisibilité
- Les nombres premiers et la décomposition des nombres
- Les fractions irréductibles
La fiche de synthèse du cours
Voici la synthèse du cours au format pdf ainsi qu’une version animée au format SVG + Sozi

Version animée pour diffusion en classe ( SVG + Sozi )
Les évaluations corrigées
Les critères de divisibilité
Attention : après qu’il ait été demandé avec les nouveaux programmes de démontrer certains de ces critères en classe, ces démonstrations ne sont plus exigibles depuis l’ajustement de juillet 2018.
Toutes ces démonstrations reposent sur le sens de l’écriture décimale des entiers et sur le fait que la somme de deux multiples d’un même nombre est encore un multiple de ce nombre.
La divisibilité par 2
Commençons par un exemple générique en partant du nombre entier $latex 2~018$.
Il faut pour cela revenir au sens de l’écriture décimale :
$latex 2~018=2\times 1~000+0\times 100+1\times 10+8\times 1$
Comme $latex 1~000$, $latex 100$ et $latex 10$ sont des multiples de 2, $latex 2\times 1~000+0\times 100+1\times 10$ est un multiple de 2.
$latex 2~018=\underbrace{2\times 1~000+0\times 100+1\times 10}_{multiple\ de\ 2}+8$
Comme 8 est un multiple de 2, 2018 est aussi un multiple de 2.
Un nombre entier est un multiple de 2 si le chiffre de ses unités en écriture décimale est 0, 2, 4, 6 ou 8.
La divisibilité par 4
On utilise à nouveau le sens de l’écriture décimale :
$latex 37~824=3\times 10~000+7 \times 1~000+8 \times 100+ 2\times 10+4$
Comme $latex 10~000=4\times 2~500$, que $latex 1~000=4 \times 250$ et que $latex 1~00=4\times 25$, (toutes les puissances de 10 dont l’exposant est supérieur ou égal à 2 sont des multiples de 100 et donc des multiples de 4) on en déduit que :
$latex 37~824=\underbrace{3\times 10~000+7\times 1~000+8\times 100}_{multiple\ de\ 4}+24$
Il suffit donc que 24 soit un multiple de 4 pour que 37 824 le soit aussi.
Un nombre entier est un multiple de 4 si le nombre formé par ses dizaines et ses unités est aussi un multiple de 4.
La divisibilité par 9 et 3
On repart à nouveau sur un exemple générique.
$latex 13~456=1\times 10~000+3\times 1~000+4\times 100+5\times 10+6$
On va utiliser le fait que $latex 99$, $latex 999$, $latex 9~999$ … sont des multiples de 9.
C’est évident $latex 99=9\times 11$, $latex 999=9\times 111$, $latex 9~999=9\times 1~111$…
$latex 13~456=1\times(9~999+1)+3\times (999+1)+4\times (99+1)+5\times(9+1)+6$
$latex 13~456=\underbrace{1\times 9~999+3\times 999+4\times 99+5\times 9}_{multiple\ de\ 9}+1+3+4+5+6$
Ainsi $latex 13~456$ est un multiple de 9 si 1+3+4+5+6 en est un aussi.
Comme un multiple de 9 est aussi un multiple de 3, pour la même raison, $latex 13~456$ est un multiple de 3 si 1+3+4+5+6 est un multiple de 3.
Un nombre entier est un multiple de 3 si la somme de ses chiffres en écriture décimale est un multiple de 3.
Un nombre entier est un multiple de 9 si la somme de ses chiffres en écriture décimale est un multiple de 9.
La divisibilité par 11
Plus amusant, ce critère demande une démonstration plus astucieuse.
Repartons sur un exemple générique et son écriture décimale :
$latex 45~765=4\times 10~000+5 \times 1~000+7\times 100+6 \times 10+5$
On reprend l’idée pour la divisibilité par 9 en faisant apparaître 9, 99, 999… et la somme des chiffres.
$latex 45~765=4\times 9~999+5\times 999+7\times 99+6 \times 9+4+5+7+6+5$
Il faut maintenant étudier la divisibilité par 11 des nombres de la forme 9, 99, 999, 9999…
$latex 9=11\times 0+9$
$latex 99=11\times 9$
$latex 999=110\times 9+9$
$latex 9~999=909\times 11$
Il semblerait que en fonction du nombre de 9 dans l’écriture du nombre, celui-ci est soit un multiple de 11 soit il reste 9 quand on le divise par 11.
Derrière cela se cache les répunits ! Un répunit en écriture décimale est un nombre dont les chiffres ne sont que des 1 ! Les nombres précédents sont des produits de 9 par un repunit.
Observons ces repunits :
1 n’est pas un multiple de 11, le reste est 1 quand on le divise par 11.
11 est un multiple de 11
$latex 111=11\times 10+1$ reste 1 par 11
$latex 1~111=11\times 101$ multiple de 11
$latex 11~111=11\times 1~010+1$ reste 1 par 11
$latex 111~111=11\times 10101$ multiple de 11
Il semblerait que un repunit soit un multiple de 11 quand le nombre de 1 est pair, et que le reste soit 1 quand le nombre de 1 est im+pair.
Pour démontrer cela il suffit de se demander comment on passe d’un repunit au suivant :
$latex 11=10\times 1+1$
$latex 111=100\times 1+11$
$latex 1~111=100\times 11+11$
$latex 11~111=100\times 111+11$
Si on note $latex u_n$ le repunit constitué de $latex n$ chiffre 1, $latex n>0$ alors $latex u_{n+2}=100\times u_n+11$
Il est assez simple de montrer ce résultat :
Comme $latex u_{n+1}=10\times u_n+1$ pour $latex n>0$ on a
$latex u_{n+2}=10\times u_{n+1}+1=10\times(10\times u_n+1)+1=100\times u_n+10+1$
Comme pour $latex n>0$, $u_{n+2}=100\times u_n+11$ cela signifie que $latex u_n$ et $latex u_{n+2}$ ont le même reste dans la division par 11.
Or $latex u_1=1$ a pour reste 1 et $latex u_2=11$ à pour reste 0.
Donc un repunit est un multiple de 11 si le nombre de chiffres 1 est pair. Sinon le reste de la division par 11 est 1$
On multiplie tout cela par 9 est on en déduit que 99, 9999, 999 999… sont des multiples de 11 et que 9, 999, 99 999… on pour reste 9 dans la division par 11.
On y est presque !
$latex 45~765=4\times 9~999+5\times 999+7\times 99+6 \times 9+4+5+7+6+5$
On va utiliser une astuce géniale. Comme 999 et 9 ne sont pas des multiples de 11 mais que le reste est 9, on va les écrire sous la formes 1001-2 et 11-2. (1001 est un multiple de 11)
$latex 45~765=\underbrace{4\times 9~999+7\times 99}_{multiple\ de\ 11}+5\times (1~001-2)+6\times(11-2)+4+5+7+6+5$
Finalement
$latex 45~765=\underbrace{4\times 9~999+5\times 1~001+7\times 99+6\times 11}_{multiple\ de\ 11}-5\times 2-6\times 2+4+5+7+6+5$
$latex 45~765=\underbrace{4\times 9~999+5\times 1~001+7\times 99+6\times 11}_{multiple\ de\ 11}+4-5+7-6+5$
$latex 45~765$ est un multiple de 11 à la seule condition que 4-5+7-6+5=5 le soit, ce qui n’est pas le cas.
Un nombre entier est un multiple de 11 si la différence de la somme de ses chiffres de rang impair et de la somme de ses chiffres de rang pair est un multiple de 11.
Si la somme des chiffres de rang pair et la somme des chiffres de rang impair d’un nombre est égale, alors ce nombre est un multiple de 11
Arithmétique et algorithmique
Ce chapitre est l’occasion de présenter la notion d’algorithme. Je vous en propose deux assez simples qui permettent la mise en place de cette notion.
Ce nombre entier est-il premier ?
Objectif : déterminer si un nombre entier saisi par l’utilisateur est premier ou non
Algorithme :
Il consiste simplement à diviser le nombre entier candidat par tous les nombres entiers supérieurs ou égal à 2 qui lui sont inférieur. On teste le reste de la division euclidienne. Si ce reste est nul alors le nombre n’est pas premier. Si le nombre n’est divisible que par lui même, alors il est premier.
On peut améliorer et du coup complexifier cet algorithme en testant le quotient de la division ce qui permet de ne diviser que par les entiers inférieurs à la racine carrée du nombre entier de départ. C’est une proposition à faire aux élèves les plus compétents.
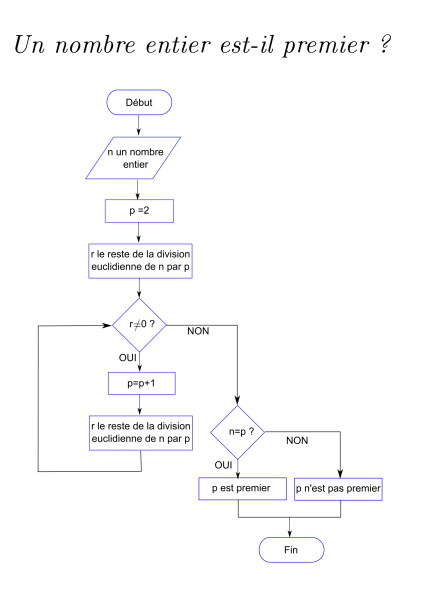
La version Algobox
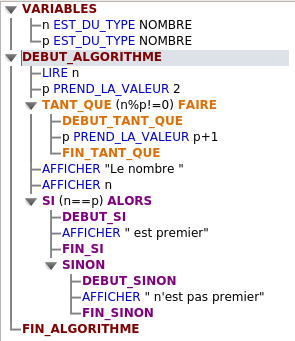
La version Scratch





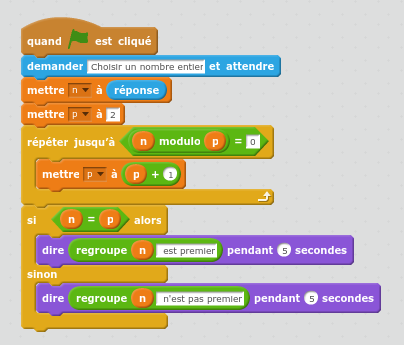










Laisser un commentaire