Hasard et intuition : je me lance dans cet article de manière un peu aléatoire…
Quand on enseigne les mathématiques il arrive souvent que l’on en vienne à discuter du hasard et des probabilités. En effet le raisonnement mathématique des probabilités semble souvent contraire à l’intuition. Hasard et intuition paraissent souvent incompatibles et celui qui connaît quelques mathématiques dans ce domaine est écouté avec circonspection à défaut de convaincre. Ainsi mes élèves doutent beaucoup quand j’affirme que la combinaison du Loto qui est sortie mercredi dernier est celle que je vais jouer cette semaine ! Ou encore que la combinaison 1, 2, 3, 4, 5 est aussi probable que 11, 15, 19, 33, 47 qui nous paraît tellement plus aléatoire !!
Bref, le sujet est vaste, hasard et intuition semblent avoir bien du mal à s’entendre.
Le plan de cet article
—
- Quelques petits problèmes troublants au sujet du hasard
- Les biais cognitifs liées aux probabilités
- Les probabilités bayesiennes
- Conclusions
—
Finalement, je me décide à écrire cet article après avoir lu avec passion les trois livres suivants :
Gérald Bronner est maître de conférence en sociologie à l’université Paris-IV où il codirige le Centre d’études sociologiques de la Sorbonne.
Pierre Spagnou est ingénieur passionné par la diffusion de la culture scientifique.
Je vais essayer d’organiser quelques idées inspirées de ces trois livres, avec mes moyens. J’espère ainsi vous donner envie de les lire pour approfondir et comprendre le sujet.
Quelques petits problèmes troublants au sujet du hasard
Dans Coincidences : nos représentations du hasard, Gérald Bronner reprends quelques problèmes issus des travaux de David Kahneman et Amos Tversky psychologues et économistes concepteurs de la théorie des perspectives pour laquelle David Kahneman obtint le prix Nobel d’économie en 2002. Ces problèmes tendent à montrer que le raisonnement humain va souvent à l’encontre du raisonnement logique des mathématiques. Ainsi en intégrant le facteur humain et des résultats expérimentaux dans la prise de décision, ces deux chercheurs ont fait entrer l’économie et la finance dans un nouveau modèle qualifié de comportemental.
Voici enfin quelques exemples :
Le problème des familles à six enfants
Premièrement un problème où hasard et intuition sont interrogés :
Dans une certaine ville on procède à une étude sur toutes les familles ayant six enfants. On observe alors l’ordre et la composition de ces naissances. On remarque que dans cette ville 72 familles ont l’ordre d’apparition suivant : FGGFGF.
La question posée est la suivante : avec cette seule information, pouvez-vous déterminer de manière approximative le nombre de familles ayant pour ordre d’apparition GGGFFF et combien avec l’ordre FFFFFF ?
Il n’y a pas de bonne réponse à ce problème. Néanmoins il faut juste signaler que même si GGGFFF ou FFFFFF nous semblent moins aléatoires que FGGFGF, ces répartitions le sont tout autant. Ainsi ces trois séries ont exactement la même probabilité d’apparition. Comme le tirage 1,2,3,4 et 5 du Loto !
Ce premier problème illustre ainsi ce que notre intuition nous dit du hasard :
- le hasard est équitable, il répartie équitablement le garçons et les filles ;
- le hasard est hétérogène, il mélange correctement les G et les F ;
- la naissance d’un garçon ou d’une fille est un phénomène aléatoire.
Finalement Gérald Bronner parle ici d’un premier biais cognitif : le hasard est juste.
Le problème des maternités
Voici un second problème :
Une ville possède deux maternités. Dans la grande 45 bébés naissent tous les jours, dans la petite 15 bébés en moyenne chaque jour. Chaque maternité note quand un jour donné plus de 60% de garçons sont nés.
Laquelle des deux maternités aura le plus de jours à plus de 60% de garçon ?
Beaucoup vont répondre que les deux maternités sont à égalité. Pourtant on sait que plus la taille de l’échantillon est important plus la fréquence approche de la probabilité théorique soit 50%. C’est donc bien dans la petite maternité que sera observé le plus de jours avec plus de 60% de garçon !
Finalement on retombe sur le caractère pseudo hétérogène du hasard.
Le paradoxe des anniversaires
Le calcul de certaines probabilités conduit à une vision particulièrement fausse du hasard. Le fameux paradoxe des anniversaires est un exemple :
Vous avez devant vous une assemblée. À partir de combien de personnes seriez-vous prêt à parier que deux d’entre elles fêtent leurs anniversaire le même jour ?
Les plus prudents répondront 365 pour ne pas perdre. Tandis que d’autres plus nombreux 182 en admettant qu’une chance sur deux soit suffisante pour les faire parier.
Finalement la réponse est étonnante et difficile/impossible à calculer de tête : à partir de 23 personnes la probabilité de gagner est supérieure à 50% !
Cependant pour calculer cette probabilités il faut faire peu de mathématiques…
Le paradoxe des anniversaires sous forme mathématiques
Ainsi calculons la probabilité de l’événement contraire : 23 personnes ont des jours de naissance tous différents.
Il y a $latex 365^{23}$ possibilités de choix de jours anniversaire.
Combien y-a-t-il de manières de choisir ces 23 jours ?
Il y a 365 possibilités pour le premier, 364 pour le second, 363 pour le troisième et … donc 343 pour la 23e jour. Soit $latex 365\times 364\times 363\times … \times 343$ possibilités.
En conclusion : la probabilité que 23 personnes aient des jours de naissances tous différents est donc :
$latex \dfrac{365\times 364\times 363\times … \times 343}{365^23}\approx 0,4927$
Voir le détail du calcul sur le calculateur Wolfram.
Ainsi dans 49,27% des cas, les 23 personnes ont des jours de naissance tous différents. D’où dans 50,73% des cas au moins 2 personnes sont nées le même jour !
Néanmoins ce calcul est hors de portée de notre intuition de par sa complexité. Le résultat ne peut qu’être étonnant !
En conclusion on peut affirmer que les coïncidences du quotidien, coïncidences pour lesquels certains veulent donner une sens caché, ne sont finalement que des exemples de notre incapacité à évaluer le hasard.
La loi des séries
Nous avons souvent le sentiment comme disais Chirac : » Les emmerdes, ça volent toujours en escadrille », que les catastrophes quand elles arrivent viennent en groupe. Le fameux jamais deux sans trois. Quand un avion s’écrase, plusieurs autres l’accompagnent la même semaine et on pourrait multiplier les exemples. À ce sujet Gérald Bronner décrit dans Coïncidences : nos représentations du hasard trois biais cognitifs responsables de ce sentiment.
Quelques biais cognitifs liées aux probabilités
Le biais de confirmation
La tâche de sélection de Wason
Voici une expérience, la tâche de sélection de Wason, qui illustre ce premier biais :

Quatre cartes comportent une lettre sur une face, un chiffre sur l’autre. Elle sont posées une face cachée sur une table comme ci-dessus. Quelles cartes faut-il retourner pour vérifier la véracité de la règle suivante : si une carte à un D sur une face, elle a un 5 sur l’autre.
La plupart des personnes effectuant ce test ( 80% ) déclarent vouloir retourner la première et la troisième carte. Evidemment retourner la première carte est légitime mais retourner la troisième ne sert à rien pour notre règle. En effet s’il y a un K au dos de la troisième carte, cela ne contredit pas la règle. C’est une confusion entre cause et conséquence. En fait il faut retourner la deuxième carte. Si sa face cachée est un D cela contredit la règle.
Proposition et proposition contraposée
En mathématiques on parlera de proposition et de proposition contraposée. Si A implique B alors Non B implique Non A. Dans notre cas si D implique 5 alors Non 5 implique Non D. Un exemple que j’utilise souvent en classe concerne cette proposition pour illustrer la notion de contraposée et de réciproque
Si nous sommes le 25 décembre alors nous sommes en vacances.
La réciproque est fausse car :
Si nous sommes en vacances alors nous ne sommes pas forcément le 25 décembre.
Par contre la proposition contraposée est vraie :
Si nous ne sommes pas en vacances alors nous ne sommes pas le 25 décembre.
Finalement, cette erreur correspond au biais de confirmation. Nous cherchons à valider une hypothèse en recueillant des informations qui la confirme. Nous recherchons beaucoup plus rarement à tester notre idée par des contre-exemples. Ainsi les croyants en l’astrologie ne manqueront pas de vous citer toutes les prédictions exactes que leur voyant préféré aura su deviner dans sa boule de cristal… oubliant par la même les nombreuses autres prédictions qui ne se sont pas réalisées. Ainsi les chaines d’informations en continue tombent aussi dans ce biais en focalisant sur certains thèmes confortant l’idée que quand un train déraille alors quelques autres vont aussi dérailler d’où ce sentiment de loi des séries.
Le biais cognitifs de la négligence de la taille de l’échantillon
Cette fois-ci je tire un exemple issue du libre de Pierre Spagnou : Raisonner probabilités, sans vous faire piéger !
Une enquête menée en Suisse sur les sports de montagne révéle que sur 10 ans il y a eu en moyenne chaque année 45 décès de randonneurs contre 6 en parapente
La randonnée en montagne est donc 7 fois plus dangereuse que le parapente !

On comprend bien sur ici que la taille de l’échantillon est en jeu. Il y a bien plus de randonneurs que de parapentistes. La même étude nous donne une idée du nombre de pratiquants, 51244 randonneurs en montagne pour 4361 parapentistes. En fréquence on obtient 0,09% pour les décès de randonneurs et 0,14% en parapente ce qui s’approche davantage de notre intuition.
Ainsi, en négligeant la taille de l’échantillon, on en vient à obtenir une réponse contraire à l’intuition !
Le loto
Tout le monde sait que la probabilité de gagner au Loto ou à l’Euromillions est très faible : 1 chance sur 19 000 000 au Loto et 1 chance sur 116 000 000 à l’Euromillions. Lire sur ce blog l’excellent article Euromillions: gagner au loto grâce aux mathématiques. Cependant nous ne sommes pas étonnés de voir régulièrement ces événements improbables se produire, il y a des gagnants. Mais nous admettons tous que en rapport avec le nombre de français ou d’européens qui jouent la fréquence d’apparition de ces événements improbables est régulière.
Par contre si en lançant de nombreuses fois une pièces de monnaie nous voyons apparaître 10 piles successifs nous seront tentés de juger que la pièce est truquée.
La théorie de l’évolution : Darwin contre Lamarck
Gérald Bronner dans Coïncidences : nos représentations du hasard apporte une conséquence passionnante du biais de la taille de l’échantillon : notre difficulté intuitive à accepter la théorie Darwinienne de l’évolution et notre tendance implicite à lui préférer la théorie finaliste de Lamarck, et ce que nous soyons croyant ou non.
Le problème des éléphanteaux sans défense
Gérald Bronner a posé le problème suivant à une population titulaire du baccalauréat :
À l’état sauvage, certains éléphanteaux sont porteurs d’un gène qui prévient de la formation des défenses. Les scientifiques ont constatés récemment que de plus en plus d’éléphanteaux naissent porteurs de ce gène, ils n’auront donc pas de défense devenu adulte.
Comment expliquer cette situation ?
Bronner a observé plusieurs types de réponse :
- Finaliste de type 1
Les défenses ne sont plus utiles aujourd’hui, elles devaient l’être avant mais ce n’est plus le cas. C’est comme pour les poils chez les humains qui ont disparus. - Finaliste de type 2
Il y a eu une mutation génétique, puisque ça sert à rien d’avoir des défenses puisque les hommes chassent les éléphants pour cela. La peur d’être tué influe sur la génétique.
Ces deux raisonnements, que certains croient être Darwinien, représentent 72% des interviewés. Ils induisent, comme Lamarck, une hypothèse métaphysique, celle d’une force vitale qui guiderait le processus d’évolution vers une finalité divine/naturelle/… !!
De même, la question de savoir pourquoi les girafes ont un long cou est une autre question célèbre sur ce thème.
Interprétation Darwinienne du problème des éléphanteaux
Cependant l’interprétation Darwinienne est la suivante : par des mutations génétiques dues au hasard du brassage des gènes dans formation d’un nouvel individu, des caractères physiques apparaissent : un long cou chez la girafe, pas de défense chez des éléphants. Alors la sélection naturelle fait le reste, un caractère du au hasard qui donne un avantage à un individu va faire que les individus possédant ce caractère vont devenir majoritaires. Ainsi un éléphant sans défense sera moins chassé qu’un éléphant avec défense et aura un avantage pour se reproduire. Finalement le gène créant cet avantage sera transmis à sa descendance pendant que le gène de la population minoritaire finira par disparaître.
En conclusion, cet exemple illustre notre difficulté à prendre conscience de la taille de l’échantillon dans un processus aléatoire. Il illustre aussi le biais cognitif de confirmation en faisant de la cause initiale une cause finale : cause/conséquence, cette confusion est à l’origine de bien des croyances !
L’effet râteau
C’est un biais qui consiste à penser que le hasard, tel un râteau, réparti de manière uniforme les résultats aléatoires.
Cette fois-ci je me tourne vers Jean-Paul Delahaye, professeur à l’Université des sciences et technologie de Lille, chercheur au laboratoire d’informatique de Lille au CNRS. Les lecteurs de Pour la science connaissent bien ce vulgarisateur des mathématiques. Dans le livre Les inattendus mathématiques, il traite de nos difficultés à envisager le hasard.
Voici une expérience tirée de ce livre :
Simulez le choix au hasard de 12 dates dans le calendrier. Quel est l’écart minimum observé entre deux de ces dates ?
Par exemple avec la suite aléatoire suivante : 19, 94, 104, 136, 165, 180, 185, 210, 256, 260, 266, 299 l’écart minimum est 4 entre 256 et 260.
A votre avis quel est la moyenne de ces écarts minimum ?
Jean-Paul Delayahe sur 100 000 répartitions obtient une moyenne de 2,53. D’ailleurs 82,5% des tirages ont des écarts de 0, 1, 2, 3 ou 4 jours. Néanmoins ce résultat est totalement contraire à notre intuition. Ces rapprochements paraissent étranges. Finalement il montre nos difficultés avec le hasard. C’est le biais de l’effet râteau.
Le cinéma et le placement aléatoire des spectateurs
Un autre argument emprunté à Gérald Bronner. On a souvent le sentiment de voir du hasard dans certains phénomènes.
Le placement des spectateurs dans une salle de cinéma presque vide est-il aléatoire ?
On est tenté de le penser, tout comme semblent placé aléatoirement les arbres d’une forêt ou les poissons dans un banc. Néanmoins la biologie et la psychologie nous apprennent le contraire. Par exemple le hasard placerait les spectateurs dans une situation moins confortable, comme l’a montré l’exemple de Delahaye. Au contraire s’il y a de nombreuses places disponibles, les spectateurs vont favoriser leur confort en créant des distances d’intimité dans le placement. Cependant rien d’aléatoire ici, un algorithme pourrait faire cette disposition. De même pour les arbres dans une forêt qui pour des contraintes de lumières, réception de l’eau et nature du sol vont se placer de manière uniforme pour optimiser le confort de chacun.
Finalement c’est encore une illustration de l’effet râteau qui nous fait penser que le hasard produit des répartitions uniformes.
Les probabilités bayésiennes
Les probabilités bayesiennes illustrent parfaitement notre propos. Elles permettent une analyse mathématiques très peu intuitive de notre réalité, analyse reposant néanmoins sur le calcul des probabilités.
Deux problèmes très étonnants
Voici deux problèmes célèbres lu dans le livre de Pierre Spagnou : Raisonner probabilités, sans vous faire piéger !
Le problème du dépistage du SIDA
Le test Elisa permet de détecter le SIDA avec une sensibilité de 99%. Lors d’un dépistage systématique de cette maladie chez les femmes enceintes, Mme Durant a un test positif.
Quelle est la probabilité que Mme Durant soit atteinte du SIDA ?
Cette probabilité est de 19% !! Avouez que c’est totalement contre intuitif !
Le problème du test ADN et de l’assassin
Un assassinat vient d’être commis dans votre quartier. Pour trouver l’assassin la police décide de faire un test génétique sur toute la population du quartier pour le comparer aux traces ADN laissées par le coupable. On sait qu’il n’y a qu’une chance sur 1 milliard de trouver un autre individu ayant le même profil ADN que le coupable.
Le test indique que votre profil est identique à celui du coupable. Quelle est la probabilité que vous soyez coupable ?
Une nouvelle fois le résultat est contre intuitif : 9%
Ainsi nous allons voir dans la suite de cette article comment les probabilités bayésiennes nous permettent de lever cette incompréhension. D’ailleurs cela va aussi illustrer le biais qui consiste à confondre cause et conséquence, ce que nous avons nommé plus haut le biais de confirmation.
Les probabilités conditionnelles : un premier exemple avec des cartes
Pour cette partie je me plonge à nouveau dans ma référence pour ce qui concerne le calcul des probabilités : le livre de Dominique Foata et Aimé Fuchs, deux professeurs de l’université de Strasbourg, Calcul des probabilités.
Un jeu de 52 cartes et un valet rouge
Étudions l’expérience aléatoire consistant à tirer une carte au hasard dans un jeu de 52 cartes.
Considérons maintenant les deux événements suivants :
- V : la carte est un valet ;
- R : la carte est rouge ( coeur ou carreau )
La probabilité de V, notée $latex P(V)=\frac{4}{52}=\frac{1}{13}$
De même $latex P(R)=\frac{1}{4}$
Introduction aux probabilités conditionnelles
Dorénavant tenons compte d’une information supplémentaire que nous aurions avant de calculer ces probabilités.
Nous allons ainsi noté V|R l’événement la carte est un valet sachant qu’elle est rouge et R|V l’événement la carte est rouge sachant que c’est un valet. Les mathématiques appellent le calcul de ces probabilités des probabilités conditionnelles.
On peut alors simplement calculer les probabilités de chacun de ces événements.
Comme il y a deux valets rouge sur 26 cartes rouges $latex P(V|R)=\dfrac{2}{26}=\dfrac{1}{13}$
Comme il y a deux cartes rouges sur 4 valets $latex P(R|V)=\dfrac{2}{4}=\dfrac{1}{2}$
Tout d’abord on remarque une première évidence : $latex P(V|R) \neq P(R|V)$
Ceci revient finalement à comprendre que Si rouge alors valet n’est pas une proposition équivalent à Si valet alors rouge. On retrouve alors la question de cause/conséquence induit par le biais de confirmation.
Notons $latex V \cap R$ l’événement être un valet rouge, c’est l’intersection des deux ensembles V et R.
Donc $latex P(V\cap R)=\dfrac{2}{56}=\dfrac{1}{26}$
La définition des probabilités conditionnelles
En reprenant les calculs précédents on constate assez vite :
$latex P(V|R)=\dfrac{1}{26} \div \dfrac{1}{2}=\dfrac{P(V \cap R)}{P(R)}$
$latex P(R|V)=\dfrac{1}{26} \div \dfrac{1}{13}=\dfrac{P(V \cap R)}{P(V)}$
Ainsi on en déduit la formule définition de la probabilité conditionnelle de A sachant B valable pour tous événements de probabilité non nulle :
$latex P(A|B)=\dfrac{P(A\cap B)}{P(B)}$
Deux résultats intermédiaires classiques
Commençons par un résultat classique le calcul de la probabilité de la réunion de deux événements : $latex P(A\cap B)$
Dans le cas de notre jeux de carte, l’événement $latex V \cap R$ est vérifié quand la carte tirée est un valet OU une carte rouge. Comme il y a 4 valets et 26 cartes rouges, dont 2 valets rouges on trouve :
$latex P(V \cap R)=\dfrac{26+4-2}{52}=\dfrac{1}{2}+\dfrac{1}{13}-\dfrac{1}{26}=P(V)+P(R)-P(V \cup R)$
Ainsi $latex P(A \cap B)=P(A)+P(B)-P(A\cup B)$ et $latex P(A\cap B)=P(A)+P(B)$ si A et B sont disjoints.
Un second résultat dont nous aurons besoin utilise la définition de la probabilité conditionnelle :
Comme $latex P(A|B)=\dfrac{P(A\cap B)}{P(B)}$ et $latex P(B|A)=\dfrac{P(A\cap B)}{P(A)}$
On obtient alors $latex P(A \cap B)=P(A|B)P(B)=P(B|A)P(A)$
La formule de Bayes
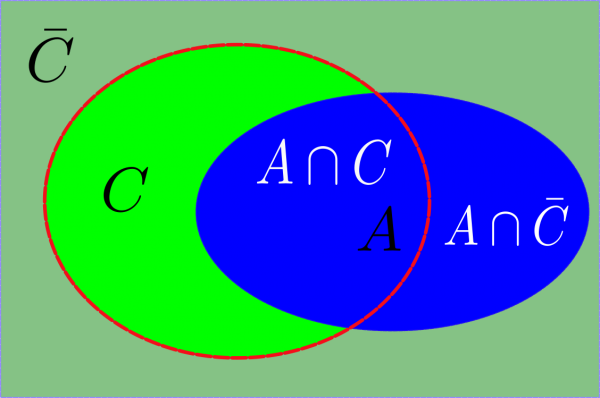
Prenons un événement C, il partage l’univers en deux parties : être dans C ou ne pas y être. On note alors $latex \bar{C}$ le contraire de C.
Ainsi tout événement A est constitué de sa partie dans C et de celle qui n’est pas dans C soit $latex A=(A\cap C) \cup (A \cup \bar{C})$
Dorénavant utilisons ce découpage de A en deux parties dans la formule de Bayes :
$latex P(C|A)=\dfrac{P(A\cup C)}{P(A)}=\dfrac{P(A\cup C)}{P(A\cap C) \cap (A \cup \bar{C})}$
Alors comme le découpage au dénominateur est disjoint on obtient :
$latex P(C|A)=\dfrac{P(A\cup C)}{P(A\cup C)+P(A\cup \bar{C})
Par conséquent en utilisant notre résultat intermédiaire :
$latex P(C|A)=\dfrac{P(A|C)P(C)}{P(A|C)P(C)+P(A|\bar{C})P(\bar{C})}$
Cette formule est connue sous le nom de formule de Bayes. Ces implications sont considérables !
Conséquences inférentielle de la formule de Bayes
En observant la formule de Bayes on constate que la probabilité de l’événement C sachant A peut se calculer à partir des événement A sachant C et A sachant Non C.
Ainsi on renverse le rôle de A et de C, la cause et sa conséquence
Finalement l’inférence Bayésienne va permettre de déduire la probabilité d’un événement à partir de probabilités déjà évaluées.
Revenons maintenant aux deux problèmes de départ pour mieux comprendre la profondeur de ce raisonnement
Le problème du dépistage du SIDA
Notons S l’événement être malade du SIDA et T l’événement avoir un test positif. La question consiste alors à déduire la probabilité de l’événement S|T , être malade du SIDA sachant que le test est positif.
La formule de Bayes nous donne donc $latex P(S|T)=\dfrac{P(T|S)P(S)}{P(T|S)P(S)+P(T|\bar{S})P(\bar{S})}$
Nous allons maintenant déduire la probabilités à partir des probabilités connues.
Reprenons ces événements un par un :
- $latex T|S$ : un test positif sachant que le patient est malade donc $latex P(T|S)=0,99
- $latex T|\bar{S} : un test positif sachant que le patient est sain, $latex P(T|\bar{S})=0,01
- S : être atteint du SIDA. d’après l’institut national de veille sanitaire il y a 150 000 personnes atteintes du SIDA/VIH en 2012 pour 65 millions d’habitants en France métropolitaine, soit $latex P(S)=\dfrac{150~000}{65~000~000}\approx 0,0023$
- $latex \bar{S}$ : ne pas être atteint par la maladie, $latex P(\bar{S})=0,9977$
Voici donc le résultat :
$latex P(S|T)=\dfrac{0,99 \times 0,0023}{0,99 \times 0,0023+0,01 \times 0,9977}\approx 0,19$
Finalement la probabilité d’avoir la maladie sachant que le test est positif est seulement de 19% !
La faible prévalence du SIDA dans la population est certainement la cause de ce résultat.
Les réseaux bayésiens
Comme on le voit dans l’exemple précédent, on peut donc déduire une probabilité en fonction d’autres éléments de connaissances. Ainsi pour les malades du SIDA, l’information concernant la prévalence de la maladie est essentielle pour terminer le calcul.
En ce qui concerne l’exemple de l’ADN et l’assassin, on avance d’un cran dans le problème. En effet il ne suffit pas de choisir deux événements T et A pour test positif et Assassin. Comme nous cherchons la probabilité de l’événement A|T, il va falloir déterminer la probabilité de T|A, c’est à dire un test positif sachant que c’est la bonne personne. Cela demande cependant de connaître le nombre éventuel de faux positifs que le test peut produire et donc d’introduire un troisième événement F qui correspond aux faux positifs du test. Finalement on peut alors parler de réseaux bayésien à trois noeux.
De manière plus pratique la probabilité P(T|A) va à son tour passer par la partition selon F et $\bar{F}$, d’où la complexité du calcul et la nécessité de la notion de réseau.
Je laisse cependant de côté les aspects techniques et vous laisse découvrir par vous même comment Pierre Spagnou dans le livre Raisonnez probabilités effectue ce calcul et montre l’usage nécessaire d’un logiciel pour traiter les calculs dans un réseau. Pour conclure sur ce thème j’ai testé Elvira un logiciel libre et gratuit qui permet de faire ce genre de calculs complexes
Conclusions
Cet article avait pour objectif de conserver quelques traces de mes lectures récentes. Nous avons vu combien notre intuition avait du mal avec les probabilités. Les raisons sont à la fois du côté de certains biais cognitif que la complexité de certains calculs comme en témoigne les réseaux bayésiens.
De plus Gerald Bronner s’interroge sur les raisons évolutionnistes et biologiques de cette difficulté à avoir un raisonnement parfaitement probabiliste. Ainsi face aux théories innéistes qui affirment que l’erreurs est substentielle à l’être humain, il oppose la diversité des erreurs et la capacité de chacun à librement consentir à certaines erreurs pour accepter et comprendre l’aléatoire quand il survient.
Enfin je ne résiste pas à vous soumettre un dernier test où les erreurs sont nombreuses pour conclure cet article. Il s’agit du Thog test d’après Wason en 1977 :
Le Thog test
Un grand ordonnateur à décidé deux caractéristiques pour qu’un objet soit un Thog : la forme et la couleur. Cependant il n’y a que deux formes possibles, le losange et le coeur et deux couleurs le bleu et le rouge. Enfin pour être un Thog un objet ne doit avoir qu’une seule de ces caractéristiques. Finalement le grand ordonnateur affirme que le losange bleu est un Thog.
Que pouvez-vous dire des figures suivantes :
- le coeur bleu ;
- le losange rouge ;
- le coeur rouge.
Pour chacun les réponses possibles sont :
- c’est un Thog ;
- ce n’est pas un Thog ;
- on ne peut pas savoir.
Sous forme de tableau voici la question reformulée :
♦ |
♥ |
♦ |
♥ |
| Thog | ? | ? | ? |
Raisonnement le plus courant
Comme le losange bleu est un Thog, la caractéristique est ainsi soit bleu soit losange. Le coeur rouge n’est donc pas un Thog. Comme le coeur bleu et le losange rouge ont une des caractéristiques, finalement ce sont des Thog. Ce qui donne :
♦ |
♥ |
♦ |
♥ |
| Thog | Thog | Thog | Non Thog |
Raisonnement classique courant
Nous avons compris que le losange bleu est un Thog, la caractéristique est ainsi soit bleu soit losange. Donc le coeur rouge n’est pas un Thog. Comme on ne sait pas si la caractéristique est coeur ou losange, finalement on ne peut pas conclure sur les deux qui restent.
♦ |
♥ |
♦ |
♥ |
| Thog | On ne sait pas | On ne sait pas | Non Thog |
Un raisonnement plus rare ( 10% des personnes testés )
On sait que le losange bleu est un Thog, donc soit le caractère losange soit le caractère bleu a été choisie comme caractéristique. Comme deux caractéristiques ne peuvent être choisies en même temps alors le coeur bleu n’est pas un Thog. En effet soit le coeur bleu soit le losange bleu aurait deux caractéristiques simultanément. Pour la même raison le losange rouge n’est pas un Thog car soit le losange bleu ou le losange rouge aurait les deux caractéristiques simultanément. Le coeur rouge n’est ni un losange, ni bleu, il possède donc l’une des deux caractéristiques que n’a pas le losange bleu. Ainsi le coeur rouge est un Thog. Finalement l’ordonnateur à choisi soit bleu et coeur soit losange et rouge.
♦ |
♥ |
♦ |
♥ |
| Thog | Non Thog | Non Thog | Thog |
Bien sûr, seul le troisième raisonnement est juste !
Ainsi l’esprit humain commet des erreurs multiples et ces erreurs dépendent du contexte, de la situation et du problème posé. Quelle liberté !














Laisser un commentaire