Les géodésiques ou le plus court chemin sur terre…
Comme tout le monde le sait, le plus court chemin pour aller d’un endroit à un autre et bien évidemment la ligne droite. J’aime à rajouter que ce fameux théorème est vrai sur le tableau de la salle de classe… mais pas sur terre… ni ailleurs !!
La raison de ce paradoxe apparent est que notre planète n’est pas plate, ce que nous savons depuis pas mal de temps déjà, nous sommes sur une sphère et les réalités géométriques ne sont pas tout à fait celles du tableau de ma salle de classe.
Je vous propose de creuser cette question en se posant le problème suivant : pour quelle raison l’avion entre l’Europe et les États-Unis ne suit pas la ligne droite que j’ai tracé sur la carte de géographie, c’est à dire un parallèle ?
Le trajet en avion entre Toulouse et Toronto
J’habite Toulouse. Nous allons donc partir de chez moi. Les coordonnées géographiques de Toulouse sont 43°36 N et 1°26 E. Pour me simplifier la vie je cherche une ville sur le continent Américain à la même latitude que Toulouse…. Première surprise, New-York est bien trop au sud ?!! À la latitude de Madrid et Rome, environ 40° N. Il faut monter plus au nord, au Canada.
Toronto est la bonne candidate pour notre expérience. Ses coordonnées sont 43°42 N et 79°24 W.
Je ne suis que professeur de collège, nous allons arrondir tout cela et dire que des longitudes et latitudes à l’unité près suffiront. Toulouse et Toronto sont donc pour cet article sur le 43 ème parallèle Nord et à 1° de longitude est pour Toulouse et 79° ouest pour Toronto.
Regardons ma carte google Map et traçons simplement les parallèles qui apparaissent comme des lignes droites, donc le plus court chemin pour les naifs !
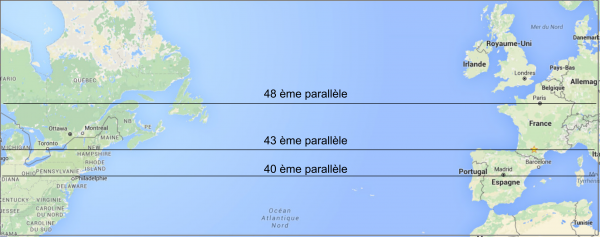
Google Map est intéressant pour les professeurs de mathématiques. Voici comment il me propose de calculer la distance entre Toulouse et Toronto.
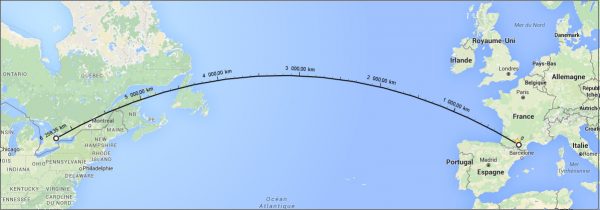
Bon ! Le plus court chemin selon Google est un arc courbé un peu étrange, loin de ma ligne droite qui suit le 43 ème parallèle. Il mesure 6258 km !
Qui a raison ? Google ou moi ?? Un peu de mathématiques seraient les bienvenues !
Le trajet Toulouse – Toronto sur la sphère
Il va maintenant falloir modéliser la situation précédente pour mieux la comprendre.
Nous allons faire l’hypothèse que le trajet s’effectue sur une sphère, la terre, dont le rayon mesure 6371 km.
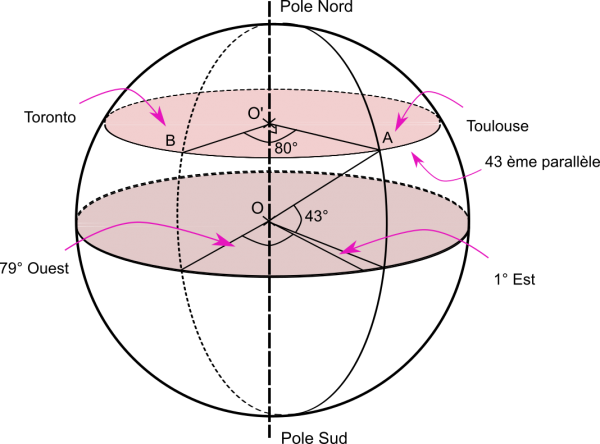
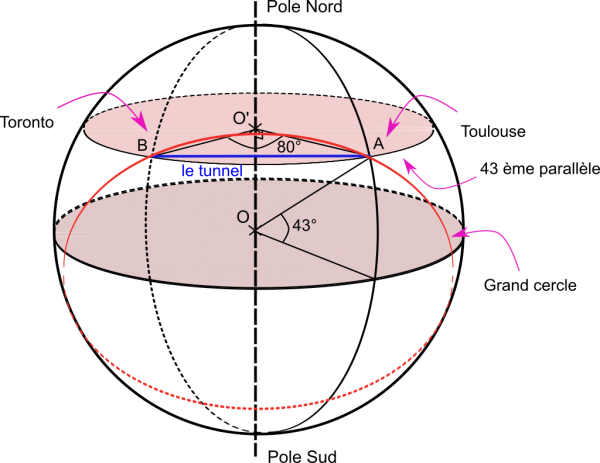
Comme Toulouse, le point A, et Toronto, le point B, sont sur la Terre, sans tenir compte de l’altitude on a ainsi OA=OB=6371 km … le rayon de la Terre.
On observe l’angle à 43° qui correspond à la latitude des deux villes. Il s’agit de l’angle qui mesure l’écart entre le plan équatorial et le plan du parallèle. On constate déjà que la ligne droite sur la carte de Google Map est en fait un arc de cercle.
On observe aussi les deux angles corresponds à la longitude des deux villes. Toulouse est à 1° Est et Toronto à 79 ° Ouest, c’est à dire de par et d’autre du méridien de Greenwitch qui marque la longitude 0°. On trouve ainsi un angle de 80°=1°+79° pour mesurer l’angle de Toronto et de Toulouse par rapport au centre du parallèle 43°.
Calcul du rayon du parallèle 43°
Dans un plan perpendiculaire au plan équatorial passant par le centre de la Terre, on constate que le triangle OO’A est rectangle en O’. Ce triangle est identique au triangle OO’B.
Un peu de trigonométrie dans le triangle OO’A rectangle en A nous montre que :
$latex cos(43^o)=\dfrac{O’A}{6371~km}$ soit $latex O’A=6371~km \times cos(43^o) \approx 4659~km$
Calcul du périmètre d’un arc de cercle sur le 43 ème parallèle
La distance que nous avons tracé en ligne droite sur la carte de Google est donc un arc du cercle de centre O’ passant par A et B. C’est un cercle de centre O’ et dont le rayon vaut environ 4659~km. Cet arc de cercle correspond à un angle de 80°. Vu depuis le plan du 43 ème parallèle on obtient ceci :

Nous allons utiliser un argument de proportionnalité. La mesure de l’arc de cercle est proportionnelle à l’angle.
Un cercle en entier est associé à un angle de 360°.
Le périmètre d’un cercle de rayon R a pour mesure $latex 2\pi R$.
L’arc entre A et B a donc pour mesure $latex \dfrac{80^o}{360^o} \times 2\pi R=\dfrac{80^o}{360^o} \times 2\pi \times 3671~km \times cos(43^o) \approx 6506~km$
Nous sommes au delà des 6258 km de Google !! Le chemin qu’il me propose serait donc plus court de près de 250 km. Comment est-ce possible ?
Creusons un tunnel entre Toulouse et Toronto
Finalement, il faut dire la vérité… Le plus court chemin entre deux points de l’espace est bien la ligne droite, c’est à dire le segment de droite qui joint les deux points.
Dans le cas de Toulouse et Toronto, le segment qui joint les deux villes est… un tunnel… qui traverse la surface terrestre…
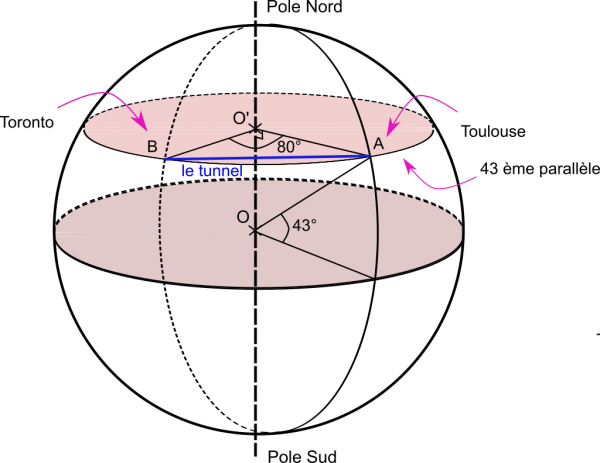
Vu depuis le plan du 43 ème parallèle on obtient ceci :

Comme A et B sont sur le cercle de centre O’ correspondant au 43 ème parallèle, O’AB est isocèle en O’. La droite (OH) est donc la médiatrice du segment [AB] et la bissectrice de l’angle à 80°.
Un peu de trigonométrie dans le triangle O’HA rectangle en H nous donne :
$latex sin(40^o)=\dfrac{HA}{6371~km \times cos(43^o)}$
$latex cos(40^o)=\dfrac{HO’}{6371~km \times cos(43^o)}$
D’où
$latex HA=6371~km \times cos(43^o) \times sin(40^o) \approx 2995~km$
$latex HO’=6371~km \times cos(43^o) \times cos(40^o) \approx 3569~km$
Comme O’H’=6371 km on a HH’=2802 km.
Ce tunnel est bien virtuel, il passe à plus de 2800 km de profondeur sous la terre !!
D’après les scientifiques il fait plus de 3000° C à cette profondeur…
Cependant ce tunnel théorique qui mesure ainsi AB=2 HA = 5990 km est bien le plus court chemin entre Toronto et Toulouse. Cette distance va nous permettre de résoudre la question de départ.
De Toulouse à Toronto sur un grand cercle
En géométrie de la sphère, un grand cercle est un cercle tracé sur la sphère dont le centre est le même centre que celui de la sphère. L’équateur et les méridiens sont des grands cercles ( les méridiens sont des demi-cercles… )
Par A, O et B il ne passe qu’un unique plan d’après la géométrie euclidienne. Dans ce plan (OAB) il existe un unique cercle de centre O passant par A et B puisque OA=OB=6371 km.
Ce cercle est le seul grand cercle passant par Toulouse et Toronto.
Reste à calculer la mesure de l’arc de cercle passant par A et B sur ce cercle.
Voici une figure dans le plan (OAB) :

Comme précédemment, OAB est isocèle en O. Dans le triangle OHA rectangle en H on peut calculer l’angle en O.
$latex sin(\widehat{HOA})=\dfrac{2995~km}{6371~km}$
On trouve ainsi une valeur approchée de l’angle $latex \widehat{HOA} \approx 28,04^o$
Au final l’angle $latex \widehat{BOA} \approx 56,08^o$
On peut alors en utilisant le même argument de proportionnalité que tout à l’heure entre l’angle et l’arc, calculer la mesure de l’arc entre A et B
$latex \dfrac{56,08^o}{360^o} \times 2 \pi \times 6371~km \approx 6236~km$
Voilà une mesure compatible avec les données de Google qui sont très dépendantes de ma précision à cliquer sur Toulouse et Toronto.
Au final voici nos résultats :
- en suivant le tunnel : 5990 km ;
- en suivant le grand cercle : 6326 km ;
- en suivant le 43 ème parallèle : 6506 km.
Voilà qui explique la trajet d’un avion entre Toulouse et Toronto… La ligne droite paraît bien courbe… Mais ce n’est qu’une illusion !
















Laisser un commentaire