Un de mes élèves de quatrième passionné par les énigmes mathématiques m’a proposé le problème suivant :
Un escargot est placé sur une corde élastique de 100 m de long. Il avance à la vitesse de 1 m à l’heure. Manque de chance cependant, un géant tire toutes les heures sur cette corde élastique et l’étire de telle manière qu’elle gagne 100 m toutes les heures. L’escargot réussira-t-il à atteindre le bout de cette corde, et le cas échéant, combien de temps mettra-t-il pour atteindre l’autre extrémité ?
Voilà un énoncé assez simple à comprendre qui réserve des surprises mathématiques de haut niveau. Je vais tenter dans cet article de faire le tour de cette question en restant dans la mesure du possible le plus simple possible dans mes explications. C’est un voyage qui nous mènera du collège au lycée et jusqu’à l’université. Nous passerons des fractions aux suites, puis nous envisagerons les séries. Nous finirons avec le logarithme népérien, l’exponentielle, l’intégrale et nous nous poserons la question du comportement asymptotique de la série harmonique… Quel marathon pour un problème d’apparence simple !
Au menu :
-
- Une première étape : à la recherche d’un propriété générale
- Quelques essais pour comprendre
- Observation au tableur de la situation
- Tentative de généralisation
- Deuxième étape : démonstration pour une étape quelconque
- Le raisonnement par récurrence
- Démonstration par récurrence pour la longueur de la corde
- Démonstration par récurrence pour la distance parcourue par l’escargot
- Troisième étape : l’escargot va-t-il atteindre le bout de la corde ?
- La série harmonique
- Un contre-exemple, le cas d’Achille et la tortue
- Divergence de la série harmonique
- La série harmonique donne le vertige
- Et l’escargot dans tout cela ?
- La constante d’Euler-Mascheroni et le logarithme népérien
- La réponse du problème du géant et de l’escargot
- Une première étape : à la recherche d’un propriété générale
Une première étape : à la recherche d’une propriété générale
Quelques essais pour comprendre
Au départ, au temps 0, l’escargot est posé sur une extrémité de la corde qui mesure 100 m.
1h plus tard, l’escargot a eu le temps d’avancer d’un mètre. À ce moment là, le géant tire sur la corde et la rallonge de 100 m. La corde passe donc de 100 m à 200 m. Sa longueur a été multipliée par 2 de manière uniforme. On en déduit que l’escargot lui aussi a profité de ce rallongement. Il se situe maintenant à 2 m de son point de départ.
2h plus tard, l’escargot a eut le temps de parcourir un mètre de plus. Il se trouve donc maintenant à 3 m de son point de départ. Le géant arrive à nouveau et tire sur la corde pour la rallonger de 100 m. Elle mesure maintenant 300 m.
Sa longueur a donc été multipliée par $\dfrac{300}{200}=\dfrac{3}{2}=1,5$.
Au final comme l’agrandissement a été uniforme, l’escargot a donc avancé de $3~m \times \dfrac{3}{2}=\dfrac{9}{2}=4,5~m$
3h plus tard, l’escargot a eut le temps de parcourir un mètre de plus. Il se trouve maintenant à 5,5 m de son point de départ. Le géant arrive à nouveau et tire sur la corde pour la rallonger de 100 m. Elle mesure maintenant 400 m.
Sa longueur a donc été multipliée par $\dfrac{400}{300}=\dfrac{4}{3}$
Au final comme l’agrandissement a été uniforme, l’escargot a donc avancé de $5,5 \times \dfrac{4}{3}=\dfrac{22}{3}~m$
Résumons la situation en notant E la distance parcourue par l’escargot et C la longueur de la corde en mètres. Pour simplifier l’écriture et la compréhension, les mathématiciens utilisent la notion de suite pour ce genre de situation. Nous allons donc noter $E_0$ et $C_0$ la distance parcourue par l’escargot et la longueur de la corde au temps 0. Nous notons de même $E_1$ et $C_1$ la distance parcourue par l’escargot et la longueur de la corde au temps 1….
Bilan :
$E_0=0$ et $C_0=100$
$E_1=2$ et $C_1=200$
$E_2=\dfrac{9}{2}$ et $C_2=300$
$E_3=\dfrac{22}{3}$ et $C_3=400$
Observation au tableur de la situation
Le tableur est l’outil le plus simple à notre disposition pour tester cette situation.
Sur les images qui suivent, la colonne 1 est incrémenté de 1 en 1. La cellule B3 contient =B2+100. La cellule C3 contient =(1+C2)*B3/B2. La cellule D3 contient =B3-C3.
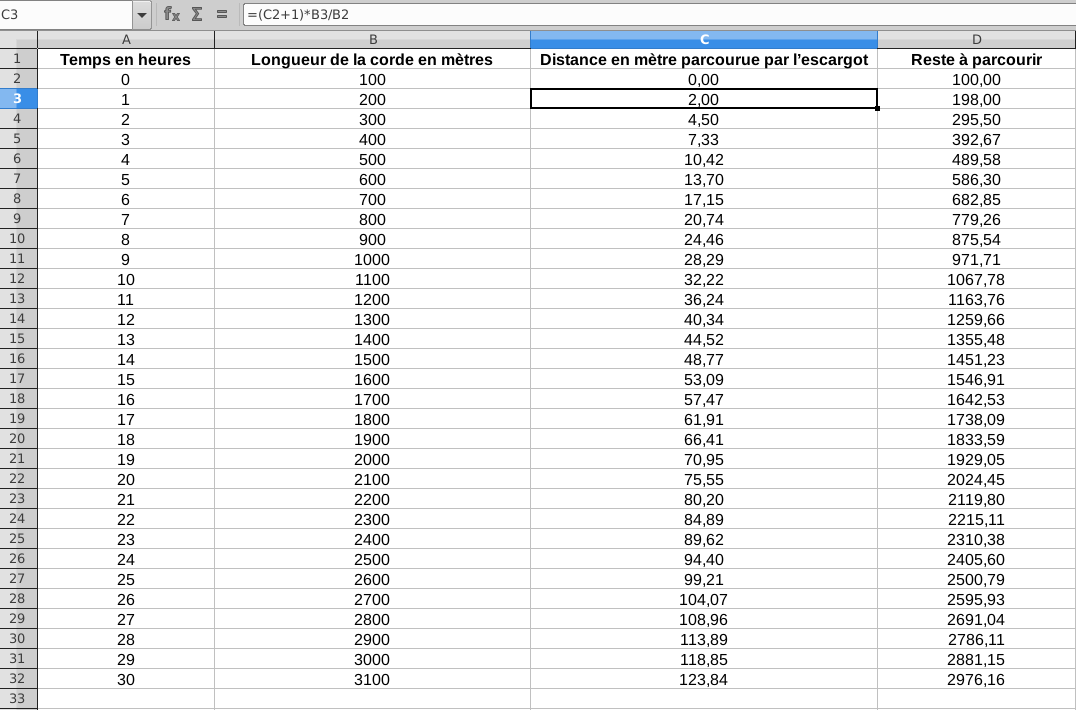
Il semblerait que l’escargot va avoir du mal à atteindre le bout de la corde. Il ne fait pas le poids !
L’escargot est bien trop lent, la corde grandit trop vite, l’écart augmente… mais malgré tout, il augmente pas tant que cela. Il semble même que la progression de l’écart se ralentit peu à peu… Il y a peut-être un espoir !
Tentative de généralisation
Nous allons tenter d’obtenir des expressions générales pour les suites $(C_n)$ et $(E_n)$.
La suite $(C_n)$ ne pose pas de difficulté.
$C_4=500$, $C_5=600$.
Pour comprendre la suite $(E_n)$, décomposons les termes :
$E_1=2\times 1=2$
$E_2=(E_1 +1)\times \dfrac{3}{2}=\dfrac{9}{2}$
$E_3=(E_2+1) \times \dfrac{4}{3}=\dfrac{22}{3}$
$E_4=(E_3+1)\times \dfrac{5}{4}=\dfrac{125}{12}$
Une idée qui peut venir à ce moment là est de repartir de $E_4$ pour redescendre vers $E_1$
$E_4=(E_3+1)\times \dfrac{5}{4}$
$E_4=E_3 \times \dfrac{5}{4}+\dfrac{5}{4}$ : on développe
On passe de $E_3$ à $E_2$ :
$E_4=\underbrace{(E_2+1)\times \dfrac{4}{3}}_{E_3} \times \dfrac{5}{4}+\dfrac{5}{4}$
$E_4=(E_2+1) \times \dfrac{5}{3}+\dfrac{5}{4}$ : le 4 a été simplifié !
$E_4=E_2 \times \dfrac{5}{3}+\dfrac{5}{3}+\dfrac{5}{4}$ : on développe.
On descend maintenant encore d’un cran et on passe à $E_1$
$E_4=\underbrace{(E_1+1)\times \dfrac{3}{2}}_{E_2} \times \dfrac{5}{3}+\dfrac{5}{3}+\dfrac{5}{4}$
$E_4=(E_1+1) \times \dfrac{5}{2}+\dfrac{5}{3}+\dfrac{5}{4}$ : le 3 a été simplifié !
$E_4=E_1\times \dfrac{5}{2}+\dfrac{5}{2}+\dfrac{5}{3}+\dfrac{5}{4}$ : on développe.
Et comme $E_1=2$ :
$E_4=2 \times \dfrac{5}{2}+\dfrac{5}{2}+\dfrac{5}{3}+\dfrac{5}{4}$
$E_4=5+\dfrac{5}{2}+\dfrac{5}{3}+\dfrac{5}{4}$
On remarque que 5 est en facteur dans chaque terme, on peut donc le factoriser :
$E_4=5 \left(1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4} \right)$
Il semble donc que nous ayons un résultat facile à généraliser pour les étapes suivantes
Deuxième étape : démonstration du résultat pour une étape quelconque
Nous avons établi des résultats jusque l’étape 4 pour les suites $(E_n)$ et $(C_n)$. Nous allons les généraliser.
Le raisonnement par récurrence
Pour cette partie il est nécessaire d’utiliser une raisonnement très particulier que l’on appelle le raisonnement par récurrence, ce que Pierre de Fermat appelait la méthode de la descente infinie. Dans notre problème, cette descente infinie est à peu près ce que l’on a fait en passant de $E_4$ à $E_1$ mais en partant cette fois-ci d’un $E_n$ quelconque avec $n$ un entier aussi grand que l’on veut.
L’idée du raisonnement par récurrence (que l’on apprend en première au lycée) est comparable à la montée d’une échelle infinie. On souhaite prouver que l’on peut monter aussi haut que l’on veut sur une échelle infinie. Il n’est pas utile pour cela de montrer que l’on peut monter sur le premier barreau, puis le second, puis le troisième… Il suffit de suivre la méthode suivante :
- Initialisation : démontrer que l’on peut monter sur le premier barreau ;
- Hypothèse de récurrence : on peut monter sur le barreau numéro $n$ pour $n$ un entier quelconque ;
- Démonstration : sachant l’hypothèse de récurrence, je peux passer au barreau suivant : $n+1$
Démonstration par récurrence pour la longueur de la corde
Grace à la première partie nous pouvons faire la conjecture suivante au sujet de la suite $(C_n)$ :
Pour $n$ un entier quelconque, $C_n=100(n+1)$
Initialisation : on a bien $C_1=100(1+1)=200$
Hypothèse de récurrence : $C_n=100(n+1)$ pour $n$ un entier quelconque
Démonstration :
À l’étape $n+1$ le géant ajoute 100 m, donc $C_{n+1}=C_n+100$
$C_{n+1}=100(n+1)+100=100n+100+100=100n+200=100(n+2)$
Ainsi $C_{n+1}=100\left[(n+1)+1\right]$
Cela démontre la conjecture !
Démonstration par récurrence pour la distance parcourue par l’escargot
La première partie du raisonnement permet de faire la conjecture suivante :
Pour $n$ un entier quelconque, $E_n=(n+1) \left( 1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+…+\dfrac{1}{n} \right)$
Initialisation : on a bien $E_1=2=2\times 1$
Même si cela ne sert à rien, on constate bien que $E_2=\frac{9}{2}=3(1+\dfrac{1}{2})$
Hypothèse de récurrence : pour $n$ un entier quelconque $E_n=(n+1) \left( 1+\dfrac{1}{2}+…+\dfrac{1}{n} \right)$
Démonstration :
À la $n+1$-ième étape, la corde passe de $C_n=100(n+1)$ à $C_{n+1}=100(n+2)$.
Le coefficient multiplicateur est donc $\dfrac{100(n+2)}{100(n+1)}=\dfrac{n+2}{n+1}$.
En tenant compte de sa progression de 1 m sur la corde on obtient le résultat suivant :
Pour $n$ un entier quelconque, $E_{n+1}=(E_n+1)\times \dfrac{n+2}{n+1}$
On utilise alors l’hypothèse de récurrence :
$E_{n+1}=\left[(n+1)\left(1+\dfrac{1}{2}+…+\dfrac{1}{n} \right)+1\right] \times \dfrac{n+2}{n+1}$
$E_{n+1}=(n+1) \times \dfrac{n+2}{n+1} \left(1+\dfrac{1}{2}+…+\dfrac{1}{n}\right)+\dfrac{n+2}{n+1}$ on développe.
$E_{n+1}=(n+2)\left(1+\dfrac{1}{2}+…+\dfrac{1}{n}\right)+\dfrac{n+2}{n+1}$
$E_{n+1}=(n+2)\left(1+\dfrac{1}{2}+…+\dfrac{1}{n}+\dfrac{1}{n+1}\right)$ : on factorise $n+2$
Ce qui prouve la conjecture !
Troisième étape : l’escargot va-t-il atteindre le bout de la corde ?
La question consiste à se demander s’il existe un rang $n$ à partir duquel $E_n \geqslant C_n$.
C’est à dire :
$(n+1)\left(1+\dfrac{1}{2}+…+\dfrac{1}{n}\right) \geqslant 100(n+1)$
$1+\dfrac{1}{2}+…+\dfrac{1}{n} \geqslant 100$
Ça y est ! Le monstre vient d’apparaître !!
Il s’agit d’une jolie métaphore : l’escargot devient un géant !
La somme à gauche dépasse t-elle le nombre 100 pour une certaine valeur de $n$ ?
La série harmonique
La somme des inverses des nombres entiers $1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+….$ est une célébrité des mathématiques. On l’appelle la série harmonique. On peut noter cette série de cette manière :
$\sum_{n=1}^{+\infty}\dfrac{1}{n}=1+\dfrac{1}{2}+\dfrac{1}{3}+…$
On note aussi souvent $H_n=1+\dfrac{1}{2}+\dfrac{1}{3}+…+\dfrac{1}{n}$
Une série est une somme infinie de termes. Une question difficile est de se demander si une série à un sens : approche t’elle d’un nombre particulier, on dit dans ce cas qu’elle converge, approche t’elle de l’infini, on dit qu’elle diverge… ou ne fait-elle rien de tout cela… ???
Une première idée intuitive consiste à penser que puisque cette somme est constituée d’une infinité de nombres tous positifs elle va forcément approcher peu à peu de l’infini positif. La réalité est un peu plus compliqué !
Une seconde idée intuitive pourrait être de penser que si les termes de la série deviennent de plus en plus proche de 0 alors forcément la série va finir par s’arrêter et s’approcher d’un nombre bien défini. Malheureusement ce n’est pas aussi simple !
Un contre-exemple : le paradoxe d’Achille et de la tortue
Je soupçonne le concepteur de l’énigme de l’escargot et du géant de s’être inspiré du paradoxe d’Achille et de la tortue énoncé par Zénon d’Élée vers 400 avant notre ère.
Zénon a écrit 8 paradoxes pour soutenir la doctrine de Parménide selon laquelle le mouvement est impossible.
Achille et une tortue font la course. Faisons l’hypothèse que la tortue avance deux fois moins vite que la tortue. Achille décide de laisser 100 m d’avance à la tortue. Zénon prétend que dans ces conditions, Achille ne rattrapera jamais la tortue.
Pour comprendre, il suffit de détailler les étapes du raisonnement :
Achille laisse 100 m d’avance à la tortue. Puis il se met à courir.
Quand il a parcouru les 100 m, la tortue a avancé. Elle a fait 50 m de plus.
Achille parcoure maintenant les 50 m qui le sépare de la tortue. Mais pendant ce temps elle a fait 25 m de plus. Etc…
Bilan de l’expérience : Achille doit parcourir $100+50+25+12,5+…$ pour rattraper la tortue.
En factorisant $100$ on arrive à :
$100\left(1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+… \right)$
Zénon suppose que cette somme, constituées de nombres positifs en quantité infini, s’approche peu à peu de l’infini. Ce qui a pour conséquence qu’Achille ne peut jamais rattraper la tortue. Ce qui contredit notre expérience courante du mouvement.
Pour lever ce paradoxe, il faut quelques connaissances sur les suites géométriques et les séries numériques.
Montrons en effet que la série $1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+…$ est convergente et tend vers $2$.
Pour $n$ un entier quelconque, la somme partielle $G_n=1+\dfrac{1}{2}+\dfrac{1}{4}+…+\dfrac{1}{2^n}$
Multiplions $G_n$ par $\left(1-\dfrac{1}{2}\right)$
$\left(1+\dfrac{1}{2}\right)G_n=\left(1+\dfrac{1}{2}\right)\left(1+\dfrac{1}{2}+\dfrac{1}{4}+…+\dfrac{1}{2^n}\right)$
$\left(1+\dfrac{1}{2}\right)G_n=1+\dfrac{1}{2}+\dfrac{1}{4}+…+\dfrac{1}{2^n}-\dfrac{1}{2}-\dfrac{1}{4}-…-\dfrac{1}{2^n}-\dfrac{1}{2^{n+1}}$
Les termes s’annulent les uns après les autres. Il reste :
$\left(1+\dfrac{1}{2}\right)G_n=1-\dfrac{1}{2^{n+1}}$
On en déduit que pour $n$ un entier quelconque :
$G_n=\dfrac{1-\dfrac{1}{2^{n+1}}}{1-\dfrac{1}{2}}$
Quand $n$ tend vers $+\infty$, $2^{n+1}$ tend aussi vers $+\infty$ et par conséquent son inverse $\dfrac{1}{2^{n+1}}$ tend vers $0$.
Ainsi quand $n$ tend vers l’infini, $G_n$ tend vers $\dfrac{1}{1-\dfrac{1}{2}}=\dfrac{1}{\dfrac{1}{2}}=2$
La série géométrique tend donc vers un nombre fini 2.
Pour en revenir à Achille, il rattrapera la tortue après 200 m de course… même si en pratique cela pose la question de diviser le réel jusque l’infiniment petit ce qui est un débat philosophique et de … physique quantique !
Concluons cette digression. Nous venons de montrer qu’Achille allait rattraper la tortue, c’est à dire que certaines séries sont convergentes. Mais qu’en est-il de la série harmonique ? Peut-elle dépasser 100 ? Diverge-t-elle jusque l’infini ?
Divergence de la série harmonique
Nicole Oresme, mathématicien allemand du moyen-âge (1320-1382) a répondu à cette question.

Voici la manière dont il s’y est pris :
Tout d’abord il est facile de voir que la suite $(H_n)$ des séries partielles de la série harmonique, est croissante. Chaque terme est supérieur au terme précédent puisque le terme ajouté est positif.
Donc $H_1<H_2<H_3<H4…$
$H_1=1$
$H_2=1+\dfrac{1}{2}$
$H_4=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}$
Or $\dfrac{1}{3}>\dfrac{1}{4}$ donc $H_4>1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{4}$
$H_4>1+\dfrac{1}{2}+\dfrac{1}{2}$
De même :
$H_8=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}$
On a toujours $\dfrac{1}{3}>\dfrac{1}{4}$ et $\dfrac{1}{5}>\dfrac{1}{8}$, $\dfrac{1}{6}>\dfrac{1}{8}$, $\dfrac{1}{7}>\dfrac{1}{8}$
On en déduit la minoration suivante :
$H_8>1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{8}+\dfrac{1}{8}$
$H_8>1+\dfrac{1}{2}+\dfrac{2}{4}+\dfrac{4}{8}$
$H_8>1+\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}$
Il y a donc un lien entre les puissances de 2 et la série harmonique.
Nicolas Oresme en déduit de la même manière que :
$H_{16}>1+\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}+\dfrac{1}{2}$
Et plus généralement que pour $n$ un entier quelconque :
$H_{2^n}>1+n \times \dfrac{1}{2}$
Quand $n$ tend vers l’infini, $1+n\times \dfrac{1}{2}$ tend aussi vers l’infini.
Cela prouve que la quantité $H_{2^n}$ tend vers l’infini quand $n$ tend vers l’infini.
La série harmonique diverge vers $+\infty$
La série harmonique donne le vertige !
La série d’Achille et de la tortue était la somme des inverses des puissances de 2 :
$1+\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+…$
Nous avons vu qu’elle approchait du nombre $2$ lorsque l’on ajoute de plus en plus de termes. Ainsi :
$\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{8}+\dfrac{1}{16}+…. \longrightarrow 2-1=1$
On peut remarquer au passage que cette série est complètement incluse dans la série harmonique !
De même on peut jouer avec inverses des puissances des nombres premiers (nombres entiers divisibles par 1 et eux même seulement !). En s’inspirant de ce que nous avons fait avec Achille, on arrive facilement à :
Pour le nombre premier 3 :
$1+\dfrac{1}{3}+\dfrac{1}{9}+\dfrac{1}{27}+\dfrac{1}{3^4}+… \longrightarrow \dfrac{1}{1-\dfrac{1}{3}}=\dfrac{3}{2}$
$\dfrac{1}{3}+\dfrac{1}{9}+\dfrac{1}{27}+\dfrac{1}{3^4}+… \longrightarrow \dfrac{1}{2}$
Pour le nombre premier 5 :
$1+\dfrac{1}{5}+\dfrac{1}{25}+\dfrac{1}{125}+\dfrac{1}{5^4}+… \longrightarrow \dfrac{1}{1-\dfrac{1}{5}}=\dfrac{5}{4}$
$\dfrac{1}{5}+\dfrac{1}{25}+\dfrac{1}{125}+\dfrac{1}{5^4}+… \longrightarrow \dfrac{1}{4}$
Il est amusant de constater que toutes les séries construites ainsi sont incluses dans la série harmonique.
Dernière série amusante, celle des inverses des nombres premiers :
$1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}+\dfrac{1}{11}+\dfrac{1}{13}+\dfrac{1}{17}+… \longrightarrow +\infty$
Une preuve de ce fait a été proposée par Paul Erdos, un mathématicien du XX ième siècle.
Et l’escargot dans tout cela ?
Pour que l’escargot atteigne le bout de la corde élastique, il faut que la série harmonique dépasse le nombre 100 à partir d’un certain rang.
Nous venons de prouver que cela arrive.
Oui, l’escargot va atteindre le bout de la corde, malgré le géant.
Soyons un peu plus précis et déterminons la valeur de $n$ pour laquelle cela arrive, pour notre problème c’est le temps nécessaire à cet exploit.
Comme pour $n$ un entier quelconque on a :
$H_{2^n}>1+n \times \dfrac{1}{2}$
On en déduit que pour $n=200$ on a :
$H_{2^{200}}>1+100>100$
$2^{200}=1 606 938 044 258 990 275 541 962 092 341 162 602 522 202 993 782 792 835 301 376 \approx 1,607 \times 10^{60}$
Ce résultat est une première approximation, car c’est une minoration. Cela signifie que pour $n=2^{200}$ on sait que l’escargot est arrivé au bout. Mais cela a certainement eu lieu bien avant.
Quand exactement ?
La constante d’Euler-Mascheroni et le logarithme népérien
Il y a une manière plus optimale de s’approcher de la série harmonique. Elle utilise la notion d’intégrale.
L’idée consiste à interpréter la série harmonique comme la somme des aires de rectangles dont un côté mesure une unité et dont l’autre côté correspond aux inverses des nombres entiers. Cette manière de faire permet naturellement de se questionner sur l’aire sous la courbe qui représente la fonction inverse.
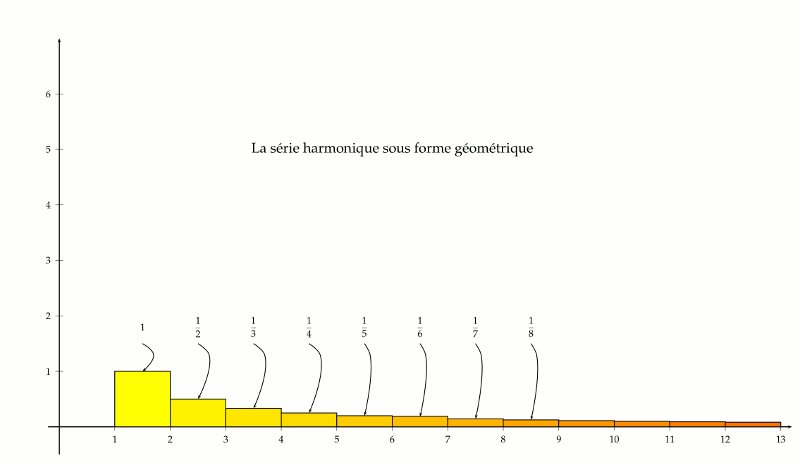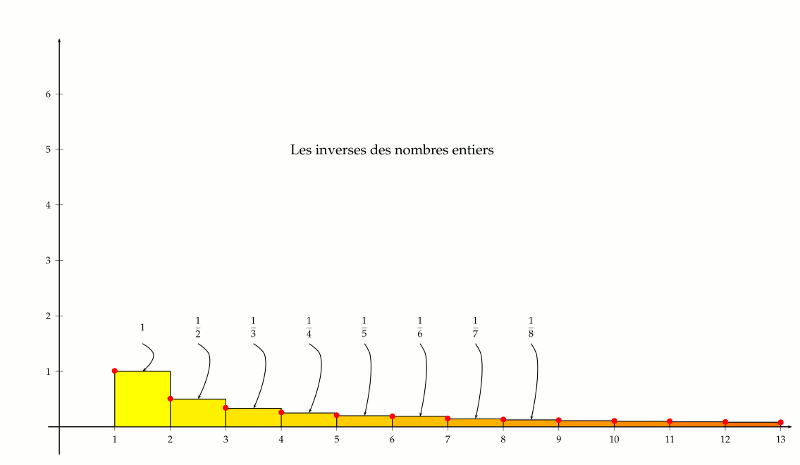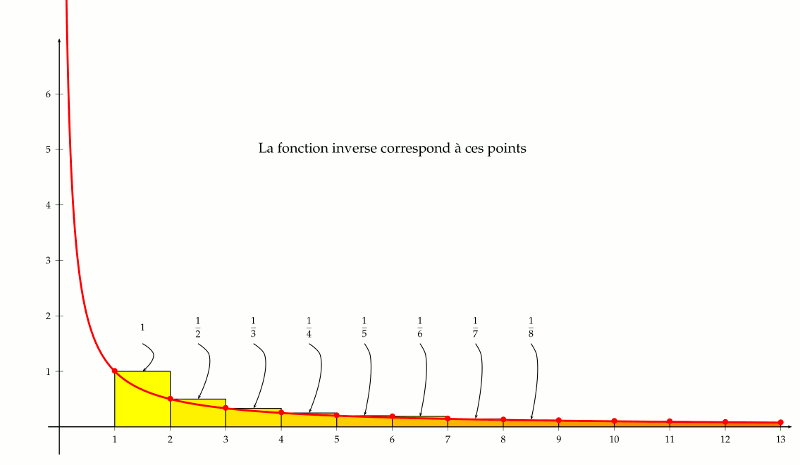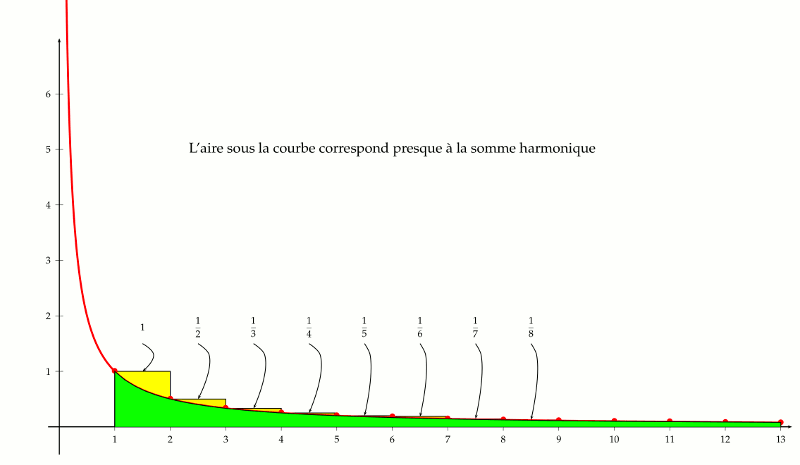
Comme on le constate sur la figure ci-dessus, il y a un petit écart entre l’aire sous la courbe et la série harmonique. Plus précisément, la série harmonique est supérieure à l’aire sous la courbe de la fonction inverse prise à partir de l’abscisse 1.
Nous avons besoin d’une nouvelle fonction pour parler de cette aire sous la courbe. Par définition, et sans rentrer dans les détails de niveau terminale scientifique, cette aire permet de définir une nouvelle fonction mathématique fondamentale : le logarithme népérien. Plus précisément, pour $n$ un entier supérieur à $1$ on note $ln(n)$ le logarithme népérien de $n$, c’est à dire l’aire sous la courbe et l’axe des abscisses, de l’abscisse $1$ à l’abscisse $n$. On appelle cela une intégrale. Le logarithme népérien d’un entier $n$ supérieur à 1 est l’intégrale entre 1 et $n de la fonction inverse.
Les calculatrices de collège et de lycée ont la touche $ln$. Par exemple $ln(5) \approx 1,609$ ce qui est bien inférieur à $H_5=1+\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}=\dfrac{25}{12} \approx 2,083$
La constante d’Euler-Mascheroni mesure l’écart à l’infini entre la série harmonique et le logarithme népérien. Cette constante notée $\gamma$ vaut approximativement :
$\gamma \approx 0,577 215 664 9$
Cet écart est donc relativement petit en rapport avec notre problème d’escargot et de géant.
Nous admettrons donc que la série harmonique et la fonction logarithme népérien ont un comportement et des ordres de grandeurs assez semblables (il n’est pas utile sur ce blog de préciser ce que signifie exactement cette phrase, nous n’allons pas parler d’équivalence asymptotique des séries… on laissera cela au professeur de mathématiques de deuxième année.. ).
La réponse au problème de l’escargot et du géant
Nous savons déjà que l’escargot atteindra le bout de la corde élastique malgré le géant. Reste à savoir combien de temps cela va mettre. Il s’agit de se demander quand la série harmonique dépasse les 100 unités.
Finalement nous admettrons que se demander pour quel $n$ entier :
$H_n > 100$
Revient à se demander :
$ln(n)>100$
On peut alors expérimenter à la calculatrice, mais la croissance est extrêmement lente.
Ainsi $ln(100) \approx 4,6$ et $ln(1~000~000) \approx 13$
Nous savons depuis la classe de quatrième que l’opération qui consiste à calculer le carré d’un nombre possède une opération inverse qui est la racine carrée.
$9^2=81$ et $\sqrt{81}=9$
Donc $n^2=121$ admet une solution positive qui est $n=\sqrt{121}$, une seconde solution est l’opposé de la première.
En terminale les professeurs de mathématiques construisent de la même manière l’inverse de la fonction logarithme népérien : il s’agit de la fonction exponentielle notée $exp()$
Comme précédemment, $ln(n)=100$ a pour solution $n=exp(100)$ on note aussi $e^{100}$
Nous voici donc au bout de ce voyage en mathématique grâce à ce joli petit problème.
La réponse est impressionnante ! Oui, l’escargot atteindra le bout de la corde élastique, il mettra $exp(100)$ heures pour le faire.
$exp(100) \approx 26 881 171 418 161 354 484 126 255 515 800 135 873 611 118 \approx 2,688 \times 10^{43}$
C’est $10^{29}$ fois plus que l’âge de l’univers !
















Laisser un commentaire