Le blog de Fabrice ARNAUD

Les fractions en sixième

dimanche 7 octobre 2018

Annales du brevet

Mon cours pour le collège

Ressources pour enseigner

Fiches de mathématiques

100 exercices pour le brevet

Pour dire merci….

Avant de commencer, mes trois conseils lecture…

Article mis à jour le dimanche 7 octobre 2018 à 15:03:57

Les fractions en sixième

Les programmes officiels

Les nouveaux programmes du collège viennent d’être publié au bulletin officiel en juillet 2018. Voici ce qu’ils préconisent pour les fractions au cycle 3 dont la classe de sixième vient clore les trois années.

Attendus de fin de cycle 3

utiliser et représenter les grands nombres entiers, des fractions simples, les nombres décimaux ;
calculer avec des nombres entiers et des nombres décimaux ;
résoudre des problèmes en utilisant des fractions simples, les nombres décimaux et le calcul.

Les connaissances au programme

Nombres et calculs
(…) Les fractions puis les nombres décimaux apparaissent comme de nouveaux nombres introduits pour pallier l’insuffisance des nombres entiers, notamment pour mesurer des longueurs, des aires et repérer des points sur une demi-droite graduée. (…)
- Utiliser et représenter les grands nombres entiers, des fractions simples, les nombres décimaux
  - Connaître diverses désignations des fractions : orales, écrites et décompositions additives et multiplicatives (ex : quatre tiers ; 4/3 ; 1/3 + 1/3 + 1/3 + 1/3 ; 1 + 1/3 ; 4 x 1/3)
  - Connaître et utiliser quelques fractions simples comme opérateur de partage en faisant le lien entre les formulations en langage courant et leur écriture mathématique (ex : faire le lien entre « la moitié de » et multiplier par 1/2).
  - Utiliser des fractions pour rendre compte de partages de grandeurs ou de mesures de grandeurs.
  - Repérer et placer des fractions sur une demi-droite graduée adaptée.
  - Encadrer une fraction par deux nombres entiers consécutifs.
  - Comparer deux fractions de même dénominateur.
  - Ecrire une fraction sous forme de somme d’un entier et d’une fraction inférieure à 1.
  - Connaître des égalités entre des fractions usuelles
    (exemples : 5/10 = 1/2 ; 10/100 = 1/10 ; 2/4 = 1/2)
  - Utiliser des fractions pour exprimer un quotient.

Pour nous accompagner dans cette tâche ambitieuse voici quelques ressources Eduscol indispensables :

Fractions et nombres décimaux au cycle 3

Annexe 1 : Découverte des fractions

Annexe 2 : De la fraction simple à la fraction décimale

Annexe 3 : Introduction de l’écriture à virgule

Annexe 4 : La glissière à nombre

Annexe 5 : Le guide-âne

C’est à peu près la logique de ma progression dans cet apprentissage.

Le plan du cours

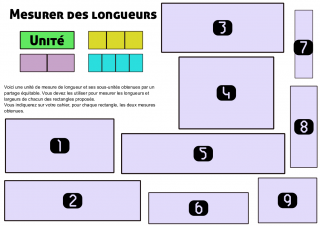
Fiche mesurer des longueurs

L’intention est de faire mesurer des grandeurs liées au rectangle en utilisant une unité arbitraire et quelques sous-unités. L’unité proposée est partagée en deux, trois et quatre.

Les objectifs :

utiliser les fractions simples pour exprimer des mesures de grandeurs ;
relier les fractions entre elles ;
écrire une mesure sous la forme d’unités entières et de partie fractionnaire ;
écrire des fractions supérieures à l’unité ;
obtenir plusieurs expressions fractionnaires pour une même grandeur.

Voici les grandeurs mesurées (exprimée en unité) sur cette fiche :

Figure n°1
- longueur : 2
- largeur : 1
Figure n°2
- longueur : $2+\frac{1}{2}$ ou $3-\frac{1}{2}$ ou $\frac{5}{2}$
- largeur : $\frac{1}{2}+\frac{1}{4}$ ou $\frac{1}{4} + \frac{1}{4} +\frac{1}{4}$ ou $\frac{3}{4}$
Figure n°3
- longueur : $2+\frac{1}{4}$ ou $\frac{9}{4}$
- largeur : $\frac{1}{3}+\frac{1}{3}+\frac{1}{4}$ ou $\frac{2}{3}+\frac{1}{4}$
Figure n°4
- longueur : $1+\frac{1}{2}+\frac{1}{4}$ ou $1+\frac{1}{4}+\frac{1}{4}+\frac{1}{4}$ ou $1+\frac{3}{4}$
- largeur : $1+\frac{1}{3}$
Figure n°5
- longueur : $3$
- largeur : $\frac{1}{2}+\frac{1}{4}$ ou $\frac{3}{4}$
Figure n°6
- longueur : $1+\frac{1}{2}+\frac{1}{3}$
- largeur : $\frac{1}{3}+\frac{1}{4}$
Figure n°7
- longueur : $\frac{1}{3}$
- largeur : $1+\frac{1}{4}$
Figure n°8
- longueur : $\frac{1}{2}$
- largeur : $1+\frac{1}{2}$
Figure n°9
- longueur : $\frac{1}{2}+\frac{1}{3}+\frac{1}{4}$ ou $1+?$
- largeur : $\frac{1}{2}+\frac{1}{3}$

7 octobre 2018

Fabrice ARNAUD

Enseigner les mathématiques au collège

4 réponses à “Les fractions en sixième”

Laurent dit :

dimanche 23 décembre 2018 à 22:10

Bonjour, merci pour votre partage. Avez-vous écrit un article sur la manière d’aborder les fractions d’une quantité ? Notamment sur sa « traduction » par une multiplication.

Répondre
- Fabrice ARNAUD dit :
  
  mardi 25 décembre 2018 à 17:53
  
  Bonjour
  
  C’est une question difficile que je souhaite traiter dans un document en cours de rédaction.
  En attendant vous trouverez une ressource fondamentale dans les documents d’accompagnement des anciens programmes :
  http://cache.media.eduscol.education.fr/file/Programmes/17/1/doc_acc_clg_calcul_numerique_109171.pdf
  Page 13
  Cordialement
  
  Répondre
  - Laurent dit :
    
    jeudi 27 décembre 2018 à 22:08
    
    Bonjour, merci beaucoup, je viens de lire votre nouvel article, très intéressant, très bien construit. J’en profite pour vous féliciter également sur votre article traitant des ratios, encore une fois très pertinent, bravo. Cordialement
    
    Répondre
    - Fabrice ARNAUD dit :
      
      dimanche 30 décembre 2018 à 19:08
      
      Merci pour vos encouragements. Les vacances sont souvent une occasion de faire une synthèse de connaissances, ce blog est l’outil que je préfère pour faire ce bilan. C’est avant tout un exercice que je m’impose pour rester à jour de ma lecture des programmes. Si en plus il est utile à certains d’entre vous…
      
      Bien cordialement
      
      Répondre