Motivations
Quand arrive la dernière quinzaine d’août, la question traditionnelle est de trouver une jolie activité pour démarrer l’année. On oublie les longs discours, les fiches de présentation et la liste de consignes inutiles. Des mathématiques et seulement des mathématiques !
Cette année, c’est une vidéo de Mickaël Launay (encore lui) qui a inspiré ce que je vais proposer à mes deux classes de sixième.
Dans cette vidéo, Mickaël Launay montre une manière surprenante de dessiner les tables de multiplication. Ce que je trouve génial ici, c’est comment une idée toute simple mène à des structures mathématiques tellement complexes. C’est un excellent moyen de montrer à des élèves jeunes ce que signifie faire des mathématiques.
Voici le lien vers cette vidéo sur Youtube : La face cachée des tables de multiplication par Mickaël Launay en juin 2015.
Description de la ressource
J’ai rédigé une fiche de travail pour les élèves de sixièmes. Je souhaite explorer avec eux les représentations graphiques des tables de multiplication de 2 à 10 dans un cercle partagé en 12 pour faire référence à l’horloge. Il est hors de question de parler d’arithmétique modulo 12, même si c’est l’idée sous-jacente et que cela me plaît beaucoup !
L’activité est guidée pour la table de 2. La lecture de la consigne devrait permettre de tracer les 11 segments. L’obstacle pour démarrer consiste à comprendre comment faire quand le produit dépasse 11. J’espère que l’analogie avec les heures permettra aux élèves de comprendre que 18 correspond au nombre 6 sur le cercle. On sait bien que 18h c’est 6h de l’après-midi ! Il faut ensuite formaliser cela en montrant que 18=12+6 et peut-être aussi que 18=12 x 1+ 6. Comme M. Jourdain, faire de l’arithmétique modulo 12 sans le savoir !
On passe ensuite aux autres tables. Un bon moyen de rafraîchir une mémoire défaillante après un été caniculaire. Le calcul modulo 12 va peu à peu se compliquer avec le nombre de tours qui augmente. J’ai ajouté en préalable la table de multiplication de 12 pour avoir quelques repères. J’imagine la difficulté pour un élève un peu fragile d’effectuer 7 x 8 = 56 puis comme 12 x 4 = 48 de se dire que 56 = 48 + 8 ! Quoi qu’il en soit, ce travail devrait permettre à tous de s’engager dans l’activité.
L’observation des 9 figures obtenues est très riche. Il y a des symétries verticales, parfois des symétries horizontales. Quelques fois, il manque des segments, car certains points reviennent sur eux-mêmes. On peut faire toute une série de conjectures et à cette occasion découvrir ce qu’est une conjecture en mathématiques.
Pour les plus persévérants, élèves et enseignants, j’ai imaginé une suite en augmentant le nombre de points sur le cercle. J’ai choisi 100 ! Pour simplifier le calcul des restes. Il faudra 100 segments pour obtenir le résultat graphique.
Je propose ces défis pour la table de 2 et la table de 3. Le résultat est époustouflant ! Pour mémoire, j’ai ajouté la correction détaillée et les figures pour 100 points pour les tables de 2 à 10. C’est très joli !
Le document
Voici le document complet, les trois fiches élèves et les corrections détaillées où j’ai ajouté quelques conjectures à signaler aux élèves.

Pour aller plus loin
Cette activité est une porte d’entrée vers de nombreuses questions mathématiques. Voici quelques pistes et quelques compléments avec lesquels je me suis amusé.
Et si on augmentait le nombre de points ?
Je propose aussi, sur cette fiche, d’observer ce qui se passe quand on augmente le nombre de points sur le cercle. Sur la deuxième et la troisième fiche, je propose 100 points !
Même si ce travail demande beaucoup de patience, le résultat vaut vraiment le coup. On voit apparaître des figures géométriques étranges : des épicycloïdes !
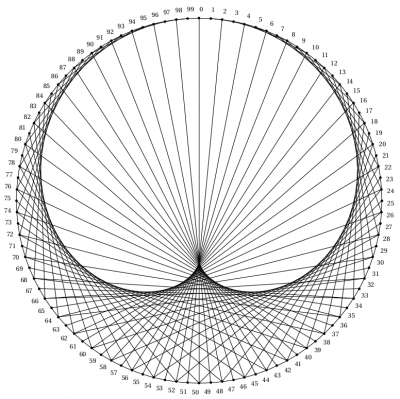
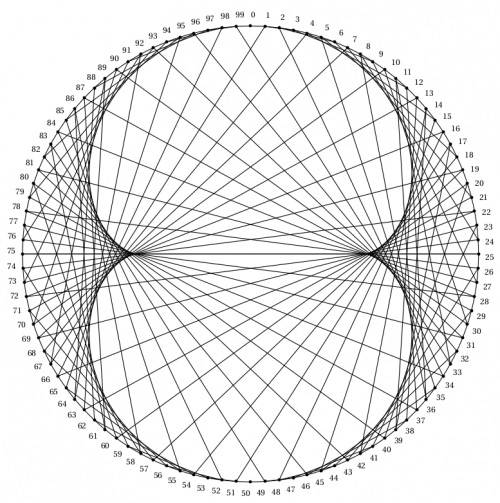
Je me suis amusé à observer ce qui se passe pour les tables suivantes. Voici le résultat :
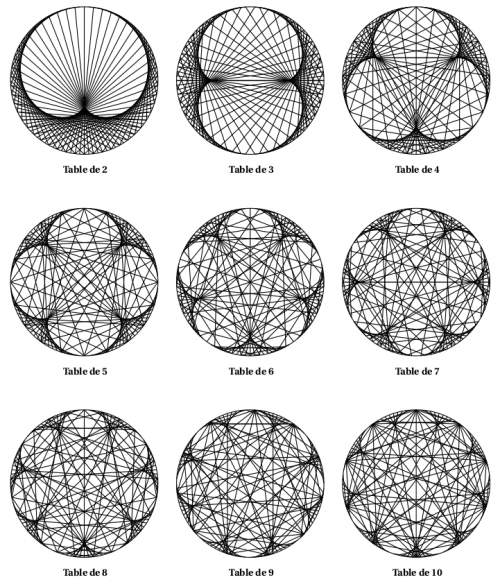
Une conjecture saute aux yeux : le nombre de bosses ou de points de rebroussement est égal au numéro de la table de multiplication ôté de 1.
Conjectures mathématiques
En observant les images obtenues avec la première partie de la fiche, on peut se poser de nombreuses questions.
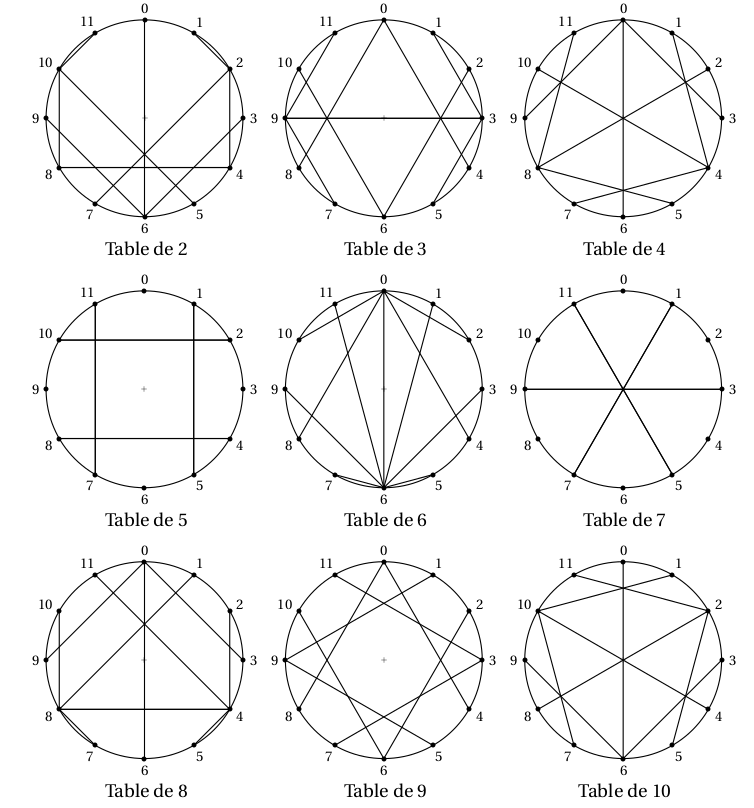
On peut faire plusieurs remarques :
- Ces figures sont symétriques par rapport à un axe vertical reliant les nombres 6 et 0 ;
- Les tables de nombres impairs présentent une symétrie horizontale ;
- Les tables de nombres pairs sont symétriques l’une par rapport à l’autre par rapport à un axe horizontal, table de 2 et table de 8, table de 4 et table de 10 ;
- Les tables de 5 et 7 sont particulières : elles ne présentent pas 11 segments, mais seulement 4 ou 3. D’ailleurs 5 et 7 sont les seuls entiers compris entre 2 et 10, premiers avec 12 !
Cette dernière remarque peut être approfondie. Quand il manque des segments, il n’y a qu’une alternative : soit un nombre mène à un autre nombre qui revient vers le premier, soit un nombre mène à lui-même.
Si nous sommes plus précis, nous pouvons constater que :
- La table de 2 est constituée de 10 segments ;
- la table de 3 est constituée de 9 segments ;
- la table de 4 est constituée de 9 segments ;
- la table de 5 est constituée de 4 segments ;
- la table de 6 est constituée de 11 segments ;
- la table de 7 est constituée de 3 segments ;
- la table de 8 est constituée de 10 segments ;
- la table de 9 est constituée de 8 segments ;
- la table de 10 est constituée de 9 segments.
On arrive à 73 segments tracés. Il devrait y en avoir 11 x 9 = 99. On remarque que seule la table de 6 permet de dessiner 11 segments. Sur l’ensemble des tables, il manque donc 26 segments que nous allons chercher.
Nous allons commencer par les points qui restent sur eux-mêmes.
Notons n le nombre sur le cercle et T la table de multiplication. On cherche n et T tel que nT congru à n modulo 12. Cela signifie que nT – n = n ( T – 1 ) congru à 0 modulo 12.
Comme 12 n’est pas premier, on sait que le groupe Z/12Z n’est pas intègre. Il possède des diviseurs de 0. Par exemple, 2 x 6 et 3 x 4 sont des produits nuls dans cet anneau. Les nombres non premiers avec 12 sont des diviseurs de zéros. On cherche les produits nuls dans cet anneau, c’est-à-dire les produits d’entiers égaux à un multiple de 12 : 12 ; 24 ; 36 ; 48 ; 60 et 72
2 x 6 ; 3 x 4 ; 3 x 8 ; 4 x 6 ; 4 x 9 ; 6 x 6 ; 6 x 8 ; 6 x 10 ; 8 x 9
Pour résoudre n ( T – 1 ) congru à 0 il faut tester les cas possibles.
- n=2 et T=7 : point isolé
- n=3 et T=5 : point isolé
- n=3 et T=9
- n=4 et T=4
- n=4 et T=7 : point isolé
- n=4 et T=10
- n=6 et T=3
- n=6 et T=5 : point isolé
- n=6 et T=7 : point isolé
- n=6 et T=9
- n=6 et T=11
- n=8 et T=4
- n=8 et T=7 : point isolé
- n=8 et T=10
- n=9 et T=5 : point isolé
- n=9 et T=9
- n=10 et T=7 : point isolé
On retrouve parmi ces 17 possibilités, on trouve les 8 points non triviaux des dessins de la table de 5 et de 7. Il en reste 9 qui sont des points qui sont un résultat de produit. Par exemple, pour la table de 9, le point 9 est relié au 1. Comme 9 x 9 = 81 = 12 x 6 + 9, 9 revient sur lui-même. C’est 1 qui donne 9.
Finalement, sur les 27 segments manquants, nous avons trouvé :
- 8 points isolés ;
- 9 points isolés invisibles puisqu’ils sont l’extrémité d’un autre segment ;
- il en manque encore…
Il nous reste à trouver les points qui en rejoignent un autre qui ensuite revient vers le point de départ. On pourrait appeler cela un segment double.
Notons n le nombre de départ et T la table. n devient n T puis n T devient n T^2. On cherche les nombres tels que n T^2 congru à n modulo 12 soit n T^2 – n ou encore n ( T^2 – 1) congru à 0 modulo 12. Comme T^2 – 1 = (T+1)(T-1) l’équation devient n (T – 1)(T + 1) congru à 0 modulo 12. On remarque que les solutions de l’étude précédente sont aussi solutions de cette équation. C’est normal puisqu’un point qui abouti sur lui-même a le même comportement quand on effectue cela deux fois. Reste à déterminer les solutions que nous n’avons pas déjà notées.
Observons T^2 – 1. On souhaite que ce soit un diviseur de zéro. En observant les carrés des entiers de 2 à 10 modulo 12 on constate que le reste est 4 pour 2 ; 4 ; 6, 8 et 10, qu’il vaut 9 pour 3 et 9 et 1 pour 5 et 7. 5 et 7 sont des nombres entiers dont le carré est congru à 1 modulo 12. Par conséquent, les 11 points du cercle pour la table de 5 et de 7 sont des solutions : ils sont soit isolés, soit l’extrémité d’un segment double.
Notons au passage que 5 et 7 sont des nombres premiers avec 12, ils sont inversibles dans Z/12Z. C’est aussi le cas de 11 puisque 11 x 11 congru à 1 modulo 12. D’ailleurs voici la table de 11…. sans surprise !
Dans l’équation n ( T – 1) ( T + 1) congru à 0 modulo 12, pour T=11 on T+1 congru à 0 modulo 12. Tous les points sont isolés ou double !
Nous pouvons donc ajouter les 7 segments doubles des tables de 5 et 7 à notre liste. Nous arrivons à 24 segments.
Il reste les produits de 3 entier, n ( T – 1 ) (T + 1) congru à 0 modulo 12. On a déjà trouvé les produits de deux facteurs nuls. Les termes T – 1 et T + 1 ont un écart de 2, cela limite nos recherches à 3 x 2 x 4 ; 6 x 2 x 4 et 9 x 2 x 4. Le cas où T=5 avec 4 x 6 étant congru à 0, ou encore 6 x 8 ont déjà été comptés. Il reste 3 x 8 x 10 ; 6 x 8 x 10 et 9 x 8 x 10. Cela fait six cas supplémentaires :
- T = 3 et n=3 , 6 ou 9 seul n=6 avait été compté
- T = 9 et n=3, 6 ou 9, ils avait déjà été compté
Nous en avons 2 segments de plus soit 26 segments ! OUF !!
Ce petit tour exhaustif en arithmétique est une source de questionnement pour les élèves en classe et accessoirement un bel exercice d’arithmétique pour les bacheliers.





Laisser un commentaire