Les transformations du plan en fin de cycle 4

Temps de lecture : 3 minutes

Les tranformations du plan dans les programmes du collège

À l’approche du brevet des collège je vous propose dans cet article une fiche de synthèse sur les connaissances à avoir acquises sur les 5 transformations du plan au programme de la fin de cycle 4 :

la symétrie axiale ( vue en sixième ) ;
la symétrie centrale ( vue en cinquième ) ;
la translation ( en quatrième ) ;
la rotation (en fin de cycle) :
l’homothétie (à l’occasion des triangles semblables en troisième ).

Voici d’ailleurs les intitulés exacts tels qu’on les trouve dans les nouveaux programmes de cycle 3 et cycle 4 depuis 2016.

Cycle 3

Connaissances et compétences associées

Exemples de situations, d’activités et de ressources pour l’élève

Compléter une figure par symétrie axiale.

Construire la figure symétrique d’une figure donnée par rapport à un axe donné que l’axe de symétrie coupe ou non la figure, construire le symétrique d’une droite, d’un segment, d’un point par rapport à un axe donné.

Figure symétrique, axe de symétrie d’une figure, figures symétriques par rapport à un axe.

Propriétés de conservation de la symétrie axiale.

Médiatrice d’un segment.

Repères de progresssivité : Un travail préalable sur les figures permet d’illustrer l’aspect global de la symétrie plutôt que de procéder de façon détaillée (par le point, le segment, la droite). Pour construire ou compléter des figures planes par symétrie, différentes procédures seront abordées au cours du cycle. Elles évoluent et s’enrichissent par un jeu sur les figures, sur les instruments à disposition et par l’emploi de supports variés.

Cycle 4

Connaissances et compétences associées	Exemples de situations, d’activités et de ressources pour l’élève
Comprendre l’effet d’une translation, d’une symétrie (axiale et centrale), d’une rotation, d’une homothétie sur une figure.	Construire des frises, des pavages, des rosaces. Utiliser un logiciel de géométrie dynamique, notamment pour transformer une figure par translation, symétrie, rotation, homothétie. Faire le lien entre parallélisme et translation, cercle et rotation.

Repères de progresssivité : La symétrie axiale a été introduite au cycle 3. La symétrie centrale est travaillée dès le début du cycle 4, en liaison avec le parallélogramme. Les translations, puis les rotations sont introduites en milieu de cycle, en liaison avec l’analyse ou la construction des frises, pavages et rosaces, mais sans définition formalisée en tant qu’applications ponctuelles. Une fois ces notions consolidées, les homothéties sont amenées en 3e , en lien avec les configurations de Thalès, la proportionnalité, les fonctions linéaires, les rapports d’agrandissement ou de réduction des grandeurs géométriques.

Le théorème de Thalès est introduit en 3e , en liaison étroite avec la proportionnalité et l’homothétie, mais aussi les agrandissements et réductions.

Il faut également consulter les documents d’accompagnements sur ce sujet :

On y apprendra quelques éléments intéressants pour le cours de mathématiques :

seule la symétrie axiale est formalisée comme une transformation ponctuelle ;
on attend que la connaissance des effets d’une rotation et d’une translation sur une figure ;
le mot vecteur et la figure flèchée sont utilisée en classe pour décrire une translation ;
l’homothétie est traitée en lien avec le théorème de Thalès et les agrandissements/réduction ;
l’homothétie de rapport négatif même si elle peut être observée au moyen de Geogebra n’a pas lieu d’être abordée au collège.

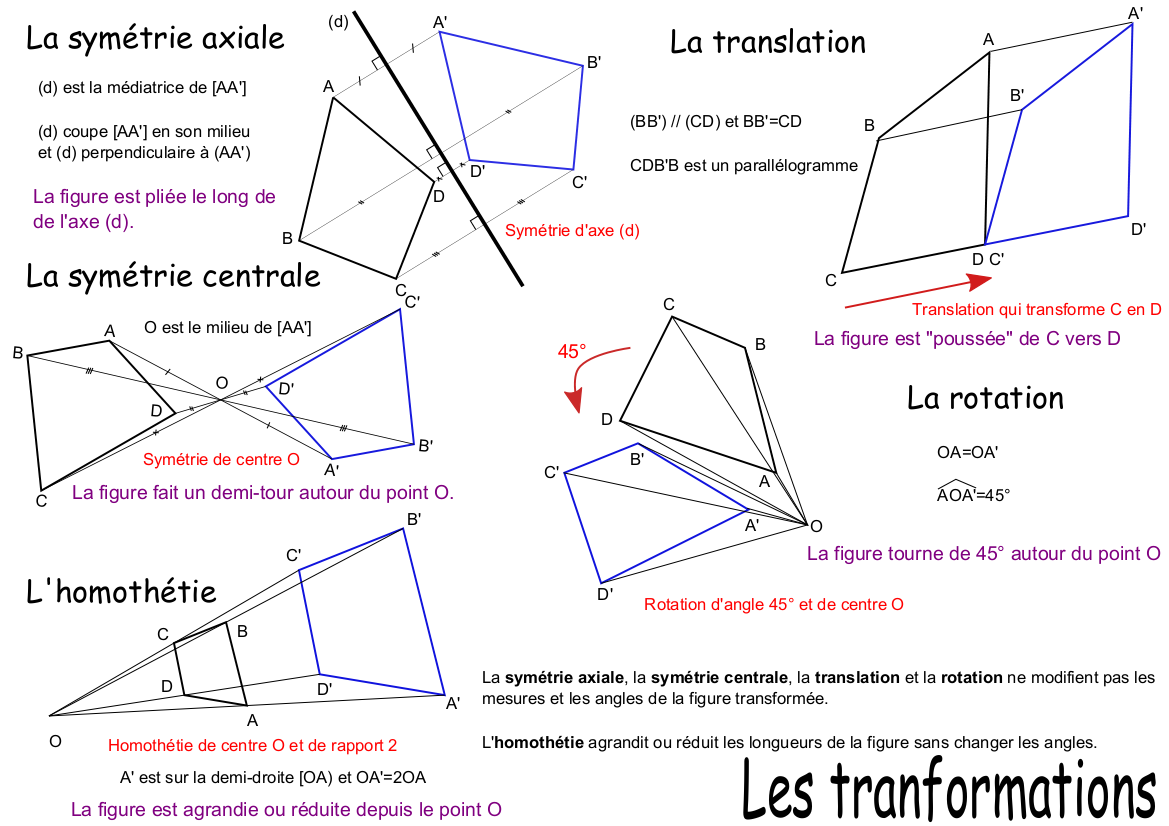
Fiche de connaissances sur les transformations du plan

En suivant ces préconisations, j’ai obtenu la fiche de synthèse suivante. Elle est disponible au format pdf pour impression, svg pour que vous puissiez la modifier (Inkscape) et sozi dans une version diaporama que j’utilise en classe.

Transformations