Voici quelques ressources pour le cours de mathématiques du collège qui concerne la sphère et la boule.
Ressources vidéos
Le film Dimensions
J’aime beaucoup utiliser cet excellent film libre de droit qui propose un voyage dans les dimensions géométriques supérieures. Il permet peu à peu de comprendre la quatrième dimension. Il est composé de neuf chapitres dont le premier peut être très utile au collège pour décrire la sphère, les parallèles, les méridiens, la latitude et la longitude. Voici la description détaillée de ce chapitre 1 tel qu’on la trouve sur le site officiel du film dimension.
https://youtube.com/watch?v=cL7BpDrRc4s%3Flist%3DPLw2BeOjATqrtiLPWvH_VeXmmBRmwcEwLz
L’aire de la sphère
Il est assez difficile sans calcul intégral de faire comprendre l’origine de la formule $latex 4\pi r^2$ qui permet de calculer l’aire de la surface de la sphère. Voici une petite sélection de ressources vidéos qui pourront nous y aider.
J’aime la démonstration pratique à base de peaux d’orange… Simple… Efficace !
Une version ficelle qui à l’intérêt de montrer le lien entre la boule et le cylindre.
https://www.youtube.com/watch?v=Fyvq-jIQKr8
Volume de la boule
Quand on a compris la formule de l’aire de la sphère, il est plus facile de passer au volume de la boule en utilisant des pyramides dont la base repose sur la sphère et de hauteur le rayon pointant toutes vers le centre. Cela ressemble à la méthode d’Archimède qui démontre la mesure de la surface du disque à partir de son périmètre et de triangles.
Voici une version dessin animé en anglais où seule la fin est nécessaire :
Voici une autre version expérimentale qui compare une boule et un cylindre de même rayon et de même hauteur. Le cylindre a donc un volume égal à $latex \pi r^2 \times 2r=2\pi r^3$. La vidéo montre que la sphère contient les $latex \dfrac{2}{3}$ du cylindre. Et comme $latex 2\pi r^3 \times \dfrac{2}{3}=\dfrac{4}{3} \pi r^3$
Enfin, ma préférée, qui montre comment passer de la formule de l’aire au volume en passant par d’infinitésimales petites pyramides à bases carrées. Vidéo en anglais mais dont le son est inutile comme dans les vidéos précédentes d’ailleurs.
Ma fiche de synthèse sur la sphère et la boule
Voici une fiche de synthèse au format pdf et vectoriel sur ce thème.
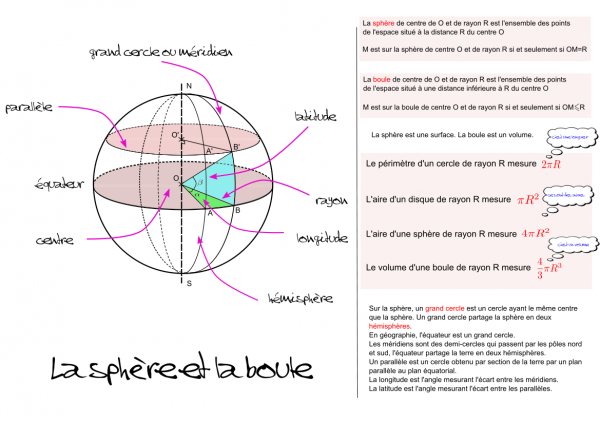
Voici la version pdf en téléchargement gratuit :






Laisser un commentaire