Même si les exercices techniques ont moins la côte, ils restent indispensables dans l’apprentissage des mathématiques dès le collège. En classe, il est essentiel de proposer des activités variées : tâches complexes, problèmes ouverts, activités de découverte, démonstration… Les exercices techniques font partie de ce cocktail. Ils permettent d’assurer les bases, de les consolider et de vérifier la progression des élèves. Ils sont même une source de plaisir pour certains. Le calcul mental est un mécanisme qui sollicite notre cerveau et lui procure souvent un sentiment de satisfaction proche de celui que l’on ressent quand on joue aux échecs ou que l’on résout un casse-tête (un rubik’s Cube !).
En écrivant ces mots, je ne peux m’empêcher de penser au film Mary (Gifted) de Marc Webb (2017) qui montre une petite fille de sept ans ayant des talents mathématiques extraordinaires. Son père lui a appris une méthode de calcul mental très efficace, la méthode Trachtenberg. Je n’avais jamais entendu parler de cette méthode avant d’avoir vu ce film. Cette méthode, que je n’ai pas pour l’instant testé par moi-même, a été inventé par Jacow Trachtenberg, un ingénieur juif, pour garder un esprit sain pendant les 7 ans qu’il a passé en camp de concentration. Cela confirme combien les mathématiques, et en particulier les aspects purement techniques, peuvent avoir un effet positif sur notre cerveau et sur celui de nos élèves.
Vous trouverez ci-dessous mes Fiches d’Exercices Gradués, FEG pour les intimes. Il s’agit de fiche d’exercices techniques de difficulté croissante. J’ai essayé d’aborder les thèmes principaux au programme du collège. Les fiches sont numérotées, graduées, par niveau de difficulté. Chacune d’entre elle est constituée :
- Un rappel de cours ;
- Quelques exemples d’usage ;
- Une quinzaine d’exercices ;
- Une correction détaillée de chaque question ;
- Quelques commentaires supplémentaires ;
- Un QR code qui mène directement à la correction ;
- Un niveau d’apprentissage pour fixer des objectifs clairs :
- Une étoile : les bases, socle commun
- Deux étoiles : attendus pour l’évaluation
- Trois étoiles : expert
- Quatre étoiles : hors catégorie.
J’utilise souvent ces fiches en classe entière. Généralement en co-enseignement avec un collègue. Chaque élève démarre avec la même fiche de départ. Les fiches suivantes sont disponibles. Les corrections sont accessibles, plastifiées au fond de la classe. Les élèves travaillent en autonomie. Ils complètent les fiches, vérifient avec la correction, se corrigent, passent à la fiche suivante. Le ou les enseignants peuvent s’occuper des élèves les plus fragiles. Les élèves les plus experts avancent à leur rythme et se lancent dans des défis de rapidité et d’exactitude.
J’ai placé quelques symboles supplémentaires pour repérer les questions les plus difficiles, voire celles qui dépassent largement les attendus. Souvent, la dernière fiche d’une série est hors catégorie, pour les passionnés. Le QR Code en haut de la fiche mène directement à la fiche corrigée en ligne hébergée sur ce blog.
Il reste forcément des erreurs et des coquilles. Si vous avez un peu de temps à m’accorder, merci de me les signaler en commentaires. Souvent mes élèves me signalent des erreurs, j’essaye de corriger le plus rapidement possible. D’autres fiches sont en cours de réalisation (toutes les transformations géométriques, les équations du premier degré et produit, Pythagore, Thalès…), soyez patients, cela demande un peu de temps.
Inutile de préciser que ces exercices sont aussi d’excellents entraînements pour préparer le brevet des collèges. Il me semble aussi qu’ils sont très utiles à ceux qui souhaitent poursuivre des études où les mathématiques auront une place importante. Calculer de manière fluide et rigoureuse est un avantage indéniable pour la compréhension de nouveaux concepts.
J’en viens à ceci, que les travaux d’écolier sont des épreuves pour le caractère, et non point pour l’intelligence. Que ce soit orthographe, version ou calcul, il s’agit de surmonter l’humeur, il s’agit d’apprendre à vouloir.
Alain
Au 2 mars 2023, vous trouverez :
- 5 thèmes traités ;
- 36 fiches corrigées ;
- 450 exercices corrigés.
Les fiches par thème
- L’ensemble de toutes les fiches au format pdf
- Les fiches par thème :
Les fiches individuelles
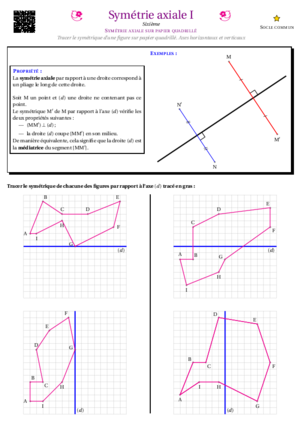
La symétrie axiale
- Symétrie Axiale I : symétrie axiale horizontale ou verticale sur papier quadrillé
- (BIENTÔT) — Symétrie Axiale II : symétrie axiale diagonale sur papier quadrillé
- (BIENTÔT) — Symétrie Axiale III : symétrie axiale horizontale ou verticale sur papier blanc
- (BIENTÔT) — Symétrie Axiale IV : symétrie axiale diagonale sur papier blanc
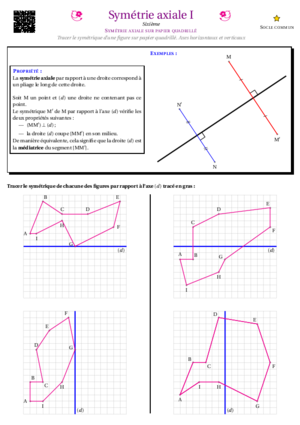
Les nombres relatifs
- Nombres Relatifs I : Sommes simples de relatifs
- Nombres Relatifs II : Sommes et notation entre parenthèses
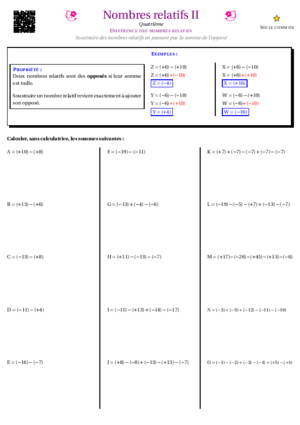
- Nombres Relatifs III : Différences et notation entre parenthèses
- Nombres Relatifs IV : Sommes algébriques avec priorité indiquée par les parenthèses
- Nombres Relatifs V : Produits et notation entre parenthèses
- Nombres Relatifs VI : Expressions algébriques et priorités opératoires
- Nombres Relatifs VII : Usage d’expressions littérales
- Nombres Relatifs VIII : Quotients
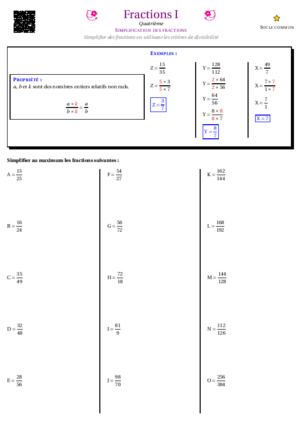
Les fractions
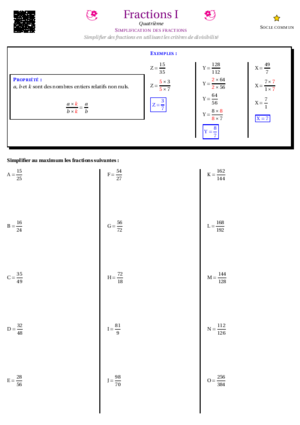
- Fractions I : Égalité de fractions
- Fractions II : Simplifications simples de fractions
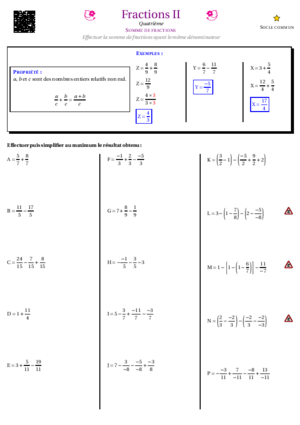
- Fractions III : Sommes de fractions ayant le même dénominateur
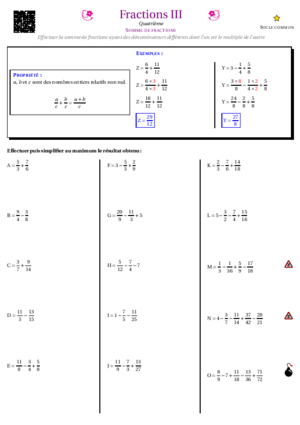
- Fractions IV : Sommes de fractions dont les dénominateurs sont multiples l’un de l’autre
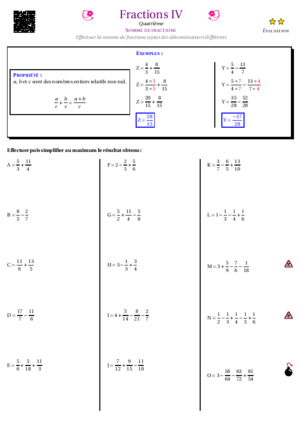
- Fractions V : Sommes de fractions cas général
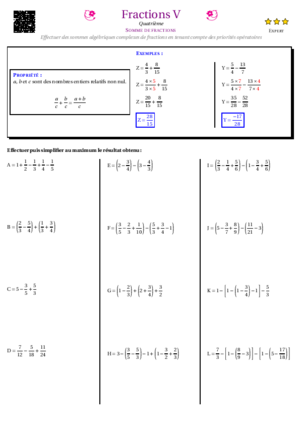
- Fractions VI : Sommes de fractions avec des priorités indiquées par des parenthèses
- Fractions VII : Produits de fractions
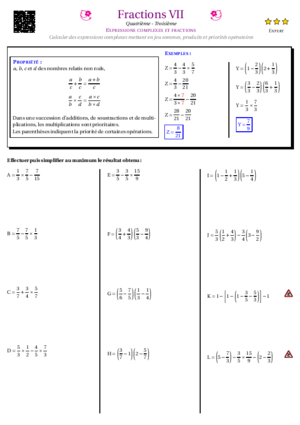
- Fractions VIII : Sommes et produits de fractions avec priorités opératoires
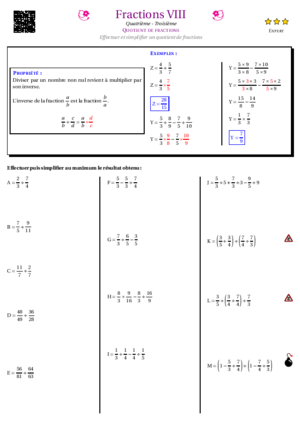
- Fractions IX : Quotient et priorités
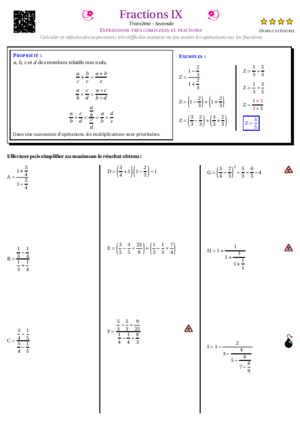
- Fractions X : Expressions très complexes avec des fractions
Les puissances
- Puissances I : Définition générale
- Puissances I : Définition des puissances de 10
- Puissances II : Produit des puissances de 10
- Puissances III : Quotient des puissances de 10
- Puissances IV : Opérations complexes sur les puissances de 10
- Puissances V : L’écriture scientifique
Le calcul littéral
- Calcul Littéral I : réduire une expression littérale
- Calcul Littéral II : opposé d’une expression littérale
- Calcul Littéral III : développer et réduire avec la simple distributivité
- Calcul Littéral IV : développer et réduire avec la simple distributivité, expressions complexes
- Calcul Littéral V : développer et réduire avec la double distributivité
- Calcul Littéral VI : développer et réduire avec la double distributivité, expressions complexes
- Calcul Littéral VII : développer et réduire une expression littérale très complexe
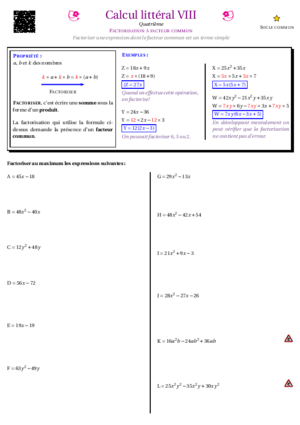
- Calcul Littéral VIII : factoriser avec un facteur commun simple
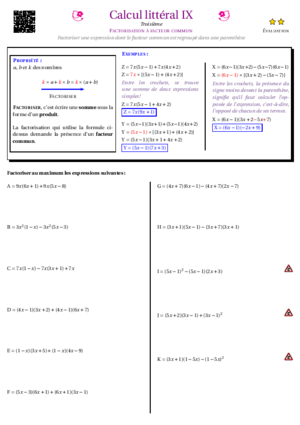
- Calcul Littéral IX : factoriser avec un facteur commun entre parenthèse
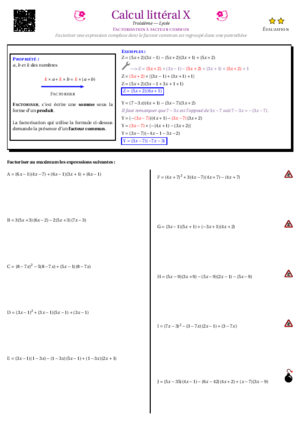
- Calcul Littéral X : factoriser avec un facteur commun, expressions complexes
- Calcul Littéral XI : développer en utilisant les identités remarquables
- Calcul Littéral XII : développer en utilisant les identités remarquables, expressions complexes
- Calcul Littéral XIII : développer et réduire des expressions très (trop) difficiles
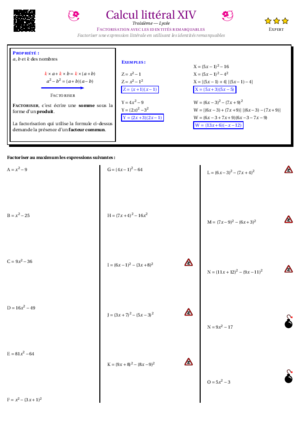
- Calcul Littéral XIV : factoriser en utilisant les identités remarquables
Les équations
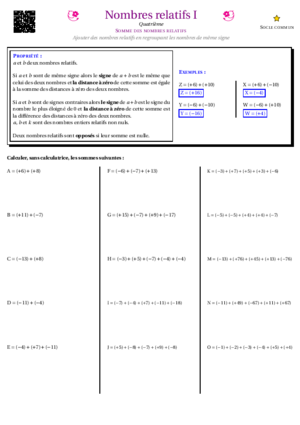
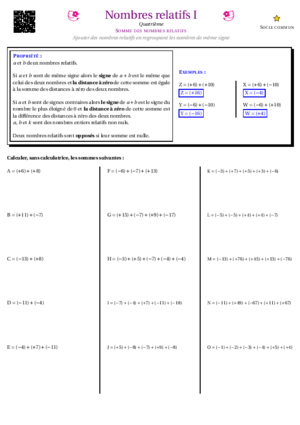
Laisser un commentaire