Le blog de Fabrice ARNAUD

Tours de magie mathématique

Les tours de magie mathématique sont une source inépuisable d’amusement. Les mathématiciens sont souvent joueurs, en tout cas ils aiment imaginer des jeux et les comprendre. Ils ont d’ailleurs inventé les probabilités pour enfin savoir les conditions exactes de gains ou de perte dans les jeux de hasard.

On peut aussi utiliser les mathématiques pour construire des petits tours de magie mathématique.

En voici une petites sélection :

Avec des nombres

Les cartes magiques

Il faut utiliser 6 cartes magiques. Voici le fichier en pdf. La même chose sous forme d’animation Sozi (appuyer sur espace).

Demander à votre victime de penser à un nombre entier entre 1 et 64 ;
Ensuite vous lui montrez les 6 cartes les unes après les autres, il doit simplement vous dire si son nombre est sur la carte ;
Une fois la sixième carte passée vous pouvez lui dire le nombre auquel il avait pensé.

Le truc est assez intéressant. Il suffit d’ajouter le premier nombre entier de chaque carte sur lesquelles le spectateur a dit oui.

Cela repose sur l’écriture en binaire des nombres entiers. Les premiers nombres des six cartes sont $1$, $2$, $4$, $8$, $16$ et $32$. Il s’agit de puissances de $2$ : $2^0=1$, $2^1=2$, $2^2=4$, $2^3=8$, $2^4=16$ et $2^5=32$.

Or tous les nombres entiers peuvent s’écrire en binaire, c’est à dire se décomposer en somme des puissances de $2$.

Par exemple $56=32+16+8$ donc $56=1\times 2^5+1\times 2^4+1\times 2^3+0\times 2^2+0\times 2^1+0\times 2^0$

$56$ est seulement sur les cartes $32$, $16$ et $8$ !

La somme magique

Dessiner sur une feuille ou un tableau un grand L à 10 cases comme sur le dessin ci-dessous :

La magicien prétend qu’il est capable d’ajouter 10 nombres entiers très rapidement, pour cela il demande à sa victime d’effectuer ceci :
Dans la case du haut demander d’écrire un nombre entier au hasard.
Dans la case juste en dessous faire écrire un deuxième nombre entier au hasard.
Dans la case en dessous on demande de faire la somme des deux premières cases.
Dans la case suivante on fait la somme de la deuxième et de la troisième case.
Et on continue jusqu’à la dixième case en bas à droite.
Au moment où la victime écrit le nombre dans la dixième case, le magicien affirme qu’il a calculé la somme des 10 nombres, il l’écrit.
On laisse alors la victime poser l’opération et péniblement vérifier que le magicien a raison !

Pour comprendre le truc il suffit de modéliser la situation :

Notons $a$ le premier nombre et $b$ le deuxième.

Dans la case 3 : $a+b$,
Dans la case 4 : $b+a+b=a+2b$
Dans la case 5 : $a+b+a+2b=2a+3b$
Dans la case 6 : $a+2b+2a+3b=3a+5b$
Dans la case 7 : $2a+3b+3a+5b=5a+8b$
Dans la case 8 : $3a+5b+5a+8b=8a+13b$
Dans la case 9 : $5a+8b+8a+13b=13a+21b$
Dans la case 10 : $8a+13b+13a+21b=21a+34b$

Quand on fait la somme des cases on obtient :

$a+b+a+b+a+2b+2a+3b+3a+5b+5a+8b+8a+13b+13a+21b+21a+34b=55a+88b$

C’est exactement 11 fois plus que la case 7… voilà comment faire facilement cette somme. Il suffit d’attendre que la case 7 soit remplie et de multiplier le résultat par 11.

Pour multiplier par 11 rapidement on peut bien sur multiplier par 10 et ajouter une fois le nombre. Mais c’est parfois difficile.

Par exemple $473 \times 11=473(10+1)=4730+473=5203$ pas si facile de tête !

On peut utiliser une méthode plus rapide…

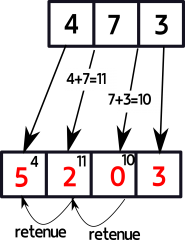
Il suffit d’ajouter les chiffres de $473$ de la gauche vers la droite.

On écrit 4, puis $4+7=11$ il y a une retenu de $1$ donc le premier chiffre du résultat est $4+1=5$

Ensuite $7+3=10$ encore une retenue que l’on ajoute à l’unité de $11$ donc $2$ pour le deuxième chiffre et $0$ pour le troisième (chiffre des unités de 10) et le quatrième est $3$ soit $5203$.

Avec des cartes

Tour de carte : les familles recomposées

Un tour purement mathématiques en 15 cartes.

Sortir du jeu 10, Valet, Dame, Roi et As dans trois couleurs, coeur, pique trefle.

Rassembler les cartes par couleur, on obtient 3 tas de 5 cartes.

Prendre une première famille, faire mélanger et les poser de gauche à droite faces cachées.

Prendre une seconde famille, mélanger et poser une carte sur chacune des 5 précédentes.

Faire de même avec la troisième famille.

Ramasser les 5 tas de 3 cartes dans n’importe quel ordre.

Faire couper le paquet plusieurs fois.

Poser face visible la carte supérieure du paquet.

Aligner de gauche à droite, faces cachées, les 7 cartes suivantes, puis poser sur chacune d’elle, de droite à gauche, les 7 dernières.

Montrer faces visibles, la troisième et la sixième paire en partant de la gauche.

Elles sont de la même couleur que la première carte sortie !

Une variante…

Sortir cette fois-ci les quatre familles, 10, Valet, Dame, Roi et As en quatre tas.

Mélanger chacun des tas.

Poser une première famille face cachée.

Distribuer sur chacune des 5 cartes posées les cartes d’une seconde famille.

Recommencer avec les deux autres familles.

Ramasser dans n’importe quel ordre les 5 paquets de 4 cartes.

Faire couper le paquet plusieurs fois.

Faire passer les cartes une à une du dessus du paquet au dessous, puis à la demande arrêter et montrer face visible la carte du dessus.

Faire passer 3 cartes sous le paquet et poser la carte suivante sur la table.

Recommencer, 3 cartes en dessous, une sur la table… quatre fois en tout.

Les quatre cartes sorties sont de la même couleur que la première sortie !

Tour de carte : le poker

Voilà comment profiter de la mode du poker pour donner une petite leçon … de tricherie. Encore un super tour de magie mathématique.

 

Prendre un jeu de 52 cartes.

Placer auparavant au sommet du jeu face cachée une quinte flush royale à coeur.

Commencer par étaler tout le jeu en ruban face cachée devant le public.

Proposer une leçon de Poker, et de probabilités en montrant combien il est difficile d’obtenir une bonne main.

Prendre 5 cartes faces cachées au hasard dans le ruban, en veillant à ne pas toucher au 5 premières.

Les montrer faces visibles, et décrire la main de Poker obtenue… rien ou une paire en général !

Placer ces 5 cartes faces cachées au sommet du ruban.

Recommencer à nouveau avec 5 autres cartes au hasard ( sans toucher aux 10 premières  ! )

Décidément, nous n’avons pas de chance au Poker.

Reposer ces 5 cartes au sommet du ruban et reformer le paquet.

Distribuer maintenant les cartes du dessus du paquet, faces cachées, en 5 mains, carte après carte, et se réserver la troisième position.

Faire retourner les mains une par une en évaluant leurs hauteurs au Poker… même discours sur le peu de chance d’avoir de bonnes mains.

Rammasser les 5 mains en veillant à commencer par celle contenant le 10 de coeur, puis le valet… jusqu’a l’As..

Redistribuer maintenant 5 mains, carte par carte, en vous réservant la troisième main.

Faire examiner les 4 autres mains, toujours aussi malchanceuses, et épiloguer sur le hasard…

Montrer enfin votre main, carte par carte, …. 10, valet, dame, roi et as de coeur !!!

…

Un tour de carte de Martin Gardner

Encore un tour de magie mathématique, un tour de carte du grand mathématicien du jeu Martin Gardner.

Prendre un jeu de 52 cartes.

Faire choisir 12 cartes faces cachées au public.

Demander de les regarder en cachette et d’en sélectionner 4.

Pendant cette phase, faire un pari. Regarder la dernière carte du paquet ( 40 cartes )  et écrire son nom sur un papier secret.

Revenir auprès du public, placer les 8 cartes non choisies sous la tas et retourner face visible les 4 cartes choisies.

On attribue une valeur numérique à chaque carte, 1 pour As, 2 pour 2… 10 pour 10 et 10 pour les figures.

Devant chaque carte face visible, pretextant un pseudo principe d’égalité, placer face cachée le complément à 10 en carte. Par exemple 7 cartes devant un 3, 4 cartes devant un 6, aucune devant un valet…

Une fois cela fait pour chaque carte, remettre ces cartes cachées sous le tas.

Faire la somme des cartes faces visibles.

Prendre le paquet et effeuiller les cartes une par une en comptant jusqu’à la somme calculée.

La carte obtenue est celle sur laquelle nous avions parié !

Un tour de cartes extraordinaire

Un tour purement mathématiques, aucune manipulation ! La magie mathématique !!!

Prendre un jeu de 52 cartes.

Faire tirer 3 cartes par le public (prendre 3 as pour les solitaires ! )

Placer l’un à côté de l’autre un premier tas de 10 cartes, un second de 15 cartes, un troisième de 15 cartes, il reste un quatrième tas de 9 cartes.

Placer face cachée la première carte choisie sur le tas de 10 cartes.

Faire couper le second tas de 15 cartes, et déposer les cartes ramassées sur la première carte choisie.

Faire poser face cachée la seconde carte sur ce qui reste du second tas.

Faire couper le troisième tas de 15 cartes, et déposer les cartes ramassées sur la seconde carte choisie.

Faire poser face cachée la troisième carte sur ce qui reste du troisième tas.

Ramasser les cartes faces cachées, en commençant par le quatrième tas de 9 cartes que l’on pose sur le troisième tas, que l’on pose sur le second, puis sur le premier.

Prendre les 4 premières cartes du paquet et les passer en dessous.

Distribuer ensuite les cartes une par une sur deux tas, faces cachées, à droite, puis à gauche, à droite, à gauche…

Éliminer le tas de droite. Il reste 26 cartes à gauche.

Recommencer à distribuer les cartes une par une sur deux tas, faces cachées, à droite, puis à gauche…

Éliminer le tas de droite. Il reste 13 cartes à gauche.

Recommencer à nouveau en commençant à droite… il reste 6 cartes à gauche.

Recommencer à nouveau en commençant à droite… il reste 3 cartes à gauche

Et ce sont les 3 cartes choisies par le public !!!

 

Si tout cela n’est pas clair, allez voir cette vidéo !

C’est fort ! Non ? C’est un beau tour de magie mathématique !

A essayer chez soi, on coupe les 15 cartes où on veut, et ça marche ! Mais pourquoi ???

Un tour avec les nombres : Danemark et Kiwi

Un petit tour de magie mathématique qui fait son effet et qui illustre l’utilité des programmes de calculs et de l’algèbre.

Choisir un membre du public avec un niveau raisonnable de culture.

Lui faire choisir en secret un nombre entier.

Lui demander de le multiplier par 3

Puis d’ajouter 7.

De multiplier le tout par 2.

D’ajouter 10 à tout cela.

De diviser ensuite par 6.

De retirer le nombre de départ.

Avec un air mystérieux, faire semblant d’espérer que ce résultat est inférieur à 26 … ( c’est 4 !!! )

Dire que 1 correspond à A, 2 à B , etc…

Demander à la victime de trouver le nom d’un pays commençant par la lettre qu’il a trouvé.

Demander ensuite de prendre la dernière lettre de ce pays et de trouver un fruit commençant par cette lettre.

Faire ensuite dire à haute voix à la victime ce qu’il vient de trouver !

Vous aviez au préalable écrit au dos du tableau ou sur une feuille la phrase  » Les Kiwis ne poussent pas au Danemark ! « 

Effet de surprise garantie !

Quelques vidéos sur des tours de cartes mathématiques