Mise à jour du 13 avril 2020
Cet article a pour objectif de vous décrire l’extension pst-eucl pour LaTeX qui permet de tracer de tracer des figures de géométrie d’un grande précision à destination des élèves de collège (et de lycée). Cette extension ne dessine pas ; elle construit la figure en définissant des relations entre les objets comme le fait par exemple Geogebra. C’est ce qui fait sont intérêt pour les enseignants de mathématiques du secondaire qui ont besoin d’exactitude quand ils produisent des figures géométrique. La lecture de cet article demande les connaissances de base pour écrire un document en LaTeX. La lecture de l’article : LaTeX au collège : écrire des mathématiques pour le secondaire pourrait vous être utile.
Ce qu’il faut savoir sur Pstricks
Pstricks est un ensemble d’extensions dédiées au dessin en Postscript pour LaTeX. Son usage demande une compilation en latex habituel, elle ne fonctionne pas immédiatement avec pdflatex (on peut cependant compiler en latex, obtenir du Postscript puis utiliser pstopdf pour obtenir du pdf… ce que je fais systématiquement !)
Pstricks permet de dessiner tout ce que l’on veut depuis un fichier source en LaTeX. Je vous laisse consulter sa documentation impressionnante sur CTAN.
Vu la complexité de cet outil, de nombreuses extensions plus géniales les unes que les autres ont été crées pour nous simplifier la vie. En voici quelques-unes que j’aime particulièrement, la plupart sont l’oeuvre d’un grand contributeur, Herbert Voß :
- pst-poker : pour dessiner des cartes à jouer ;
- pst-labo : pour dessiner des objets du laboratoire de chimie ;
- pst-geo : pour les projections de cartes de géographie ;
- pst-poly : pour les polygones ;
- pst-platon : pour les solides de platon ;
- pst-circ : pour dessiner des circuits électriques ;
- pst-vehicle : pour faire rouler sans glisser des véhicules sur une courbe (indispensable 🙂 ) ;
- pst-solarsystem : pour dessiner le système solaire à une date donnée ;
- pst-eucl : pour faire de la géométrie euclidienne ;
- …
Je crois qu’on trouve un peu tout en pstricks : des diagrammes de Gantt, UML, tableau de variations.. je vous laisse fouiller sur CTAN.
Dans cet article nous utiliserons essentiellement l’extension pst-eucl de Herbert Voß. Elle permet de construire des figures géométriques de manière euclidienne en definissant des objets puis des relations entre les objets.
Cette extension a été crée en octobre 2005 par Dominique Rodriguez. Je l’utilise depuis cette époque. Abandonné par son auteur en 2014 en version 1.51 elle a été très sérieusement reprise en main par Herbert Voß depuis 2018. Son développement est depuis très rapide avec des mises à jour plusieurs fois par an.
La dernière version est pst-eucl 1.71 du 27 février 2020.
Cette extension est installée automatiquement avec les extensions pstricks d’une distribution LaTeX.
L’extension de géométrie euclidienne : pst-eucl
Je vous propose les options les plus utiles pour les figures de géométrie utilisées au collège. Pour une liste exhaustive des possibilités de pst-eucl je vous invite à consulter la documentation sur CTAN.
L’environnement pspicture
Les commandes de l’extension pst-eucl doivent se trouver dans un environnement pspicture à l’aide de la commande suivante :
\begin{pspicture}(xmin,ymin)(xmax,ymax)
...
\end{pspicture}
Cela crée une figure de géométrie dont le coin inférieur gauche a pour coordonnée (xmin, ymin) et le coin supérieur droit (xmax,ymax). L’argument (xmin,ymin) est facultatif, il vaut (0,0) par défaut.
Si le dessin doit déborder de ce cadre, il déborde… La version étoilée de pspicture (\begin{pspicture*}(x,y)) empêche le débordement.
L’unité par défaut est le centimètre. On peut jouer avec les unités pour obtenir un agrandissement ou une réduction de la figure ce qui est pratique pour gérer sa position dans une page sans avoir à se soucier des coordonnées des points. Pour cela il faut utiliser les options unit, xunit et yunit (et même runit pour les coordonnées polaires) de pstricks.
Exemples :
\begin{pspicture}(-2,-2)(2,2)
% La commande pstricks psline permet de relier des points entre eux
\psline(-1,-1)(-1,1)(1,1)(1,-1)(-1,-1)
\end{pspicture}
Le premier carré à gauche est obtenu avec le code ci-dessus.
Le carré central avec le même code avec au préalable \psset{unit=2cm}
Le rectangle avec au préalable \psset{xunit=1cm, yunit=0.5cm}.
Le point
\pstGeonode[Options](x1,y1){A1}(x2,y2){A2}...(xn,yn){An}
Créer un ou plusieurs points aux coordonnées spécifiées portant le nom indiqué.
Voici les options les plus utiles :
- PosAngle =angle : angle orienté est compris entre 0 et 360. Il permet d’indiquer la position de la lettre par rapport au point. La valeur par défaut est 0.
- PointSymbol=symbole : le symbole pour représenter un point. Traditionnellement on utilise souvent en France une croix (PointSymbol=x) pour les figures dans le plan et un plus (PointSymbol=+) dans un repère. Le symbole par défaut est le point (PointSymbol=*). Voici la liste exhaustive d’après la documentation officielle :

- PointName=none : permet de ne pas faire apparaître le nom du point. Associé avec PointSymbol=none permet de construire un points sans qu’il apparaisse sur le dessin.
On peut fixer dès le départ les options par défaut, en ce qui me concerne j’utilise la commande
\psset{PointSymbol=+} dans l’entête de mon document ou au début de la balise \pspicture. On peut faire passer dans cette commande l’ensemble des options dont on a besoin.
Exemples :
Notez le passage d’arguments multiples avec les accolades !
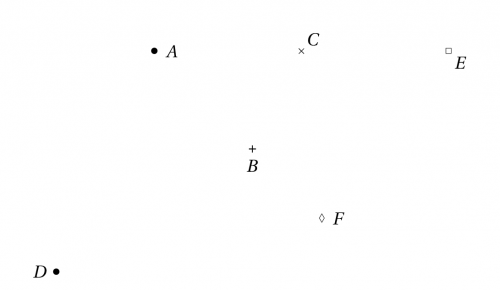
\begin{pspicture}(-5,-3)(5,3)
% Un point A(-2,2) avec les options par défaut
\pstGeonode(-2,2){A}
% Un point B(0,0) en jouant sur la position de la lettre et le symbole
\pstGeonode[PosAngle=-90, PointSymbol=+](0,0){B}
% Même chose avec C(1,2)
\pstGeonode[PosAngle=45, PointSymbol=x](1,2){C}
% Notez l'usage de l'accolade pour faire passer une option
% différente pour chaque point.
\pstGeonode[PosAngle={180,-45}, PointSymbol={*,square}](-4,-2.5){D}(4,2){E}
% Et un point en coordonnée polaire
\pstGeonode[PointSymbol=diamond](2;-45){F}
\end{pspicture}
L’option CurveType utilisable avec \pstGeonode permet de tracer automatiquement trois sortes de lignes passant par ces points :
- CurveType=polygon : trace le polygone fermé passant par ces points ;
- CurveType=polyline : trace la ligne brisée passant par ces points ;
- CurveType=curve : trace une ligne courbe passant par ces points.
\begin{pspicture}(-7,-3)(5,3)
\psset{PointSymbol=+}
% Cinq points habituels
\pstGeonode[PosAngle={-90,-90,90,90,180}](-7,-2){A}(-5,-2){B}(-5,2){C}(-6,2){D}(-7,0){E}
% Le polygone dont le sommet sont ces points
\pstGeonode[PosAngle={-90,-90,90,90,180}, CurveType=polygon, linecolor=red](-4,-2){A}(-2,-2){B}(-2,2){C}(-3,2){D}(-4,0){E}
% Le ligne brisée passant par ces points
\pstGeonode[PosAngle={-90,-90,90,90,180}, CurveType=polyline, linecolor=blue](-1,-2){A}(1,-2){B}(1,2){C}(0,2){D}(-1,0){E}
% Une courbe passant par ces points
\pstGeonode[PosAngle={-90,-90,90,90,180}, CurveType=curve, linecolor=red](3,-2){A}(5,-2){B}(5,2){C}(4,2){D}(3,0){E}
\end{pspicture}
Segment, droite et demi-droite
Objets de base
\pstLineAB[Options]{A}{B}
Tracer le segment [AB], la demi-droite [AB) ou la droite (AB).
Par défaut cette commande trace un segment. Pour tracer une demi-droite ou une droite il faut utiliser l’option suivante :
- nodesepA=abscisse : abscisse permet de contrôler la longueur de la droite (oui… concept étrange mais nécessaire pour tracer une droite).
Une valeur négative comme -1 fait débuter la droite une unité avant le premier point. Une valeur positive la fait débuter après. Par défaut cette valeur vaut 0 ; - nodesepB=abscisse : même chose mais pour le second point ;
- nodesep=abscisse : pour appliquer la même règle au niveau du premier et de second point.
Exemples :
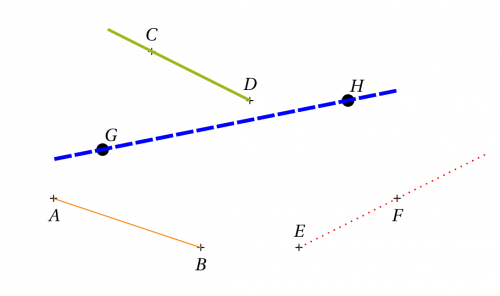
\begin{pspicture}(-5,-3)(5,3)
% Pour fixer définitivement le symbole du point
\psset{PointSymbol=+}
\pstGeonode[PosAngle=-90](-4,-1){A}(-1,-2){B}
% Un segment [AB] classique
\pstLineAB{A}{B}
\pstGeonode[PosAngle=90](-2,2){C}(0,1){D}
% Une demi-droite [DC)
\pstLineAB[nodesepA=-1]{C}{D}
\pstGeonode[PosAngle={90,-90}](1,-2){E}(3,-1){F}
% Une demi-droite [EF)
\pstLineAB[nodesepB=-2]{E}{F}
\pstGeonode[PosAngle=60](-3,0){G}(2,1){H}
% Une droite (GH)
\pstLineAB[nodesep=-1]{G}{H}
\end{pspicture}
Il y a de nombreuses options qui viennent de pstricks qui permettent de modifier l’apparence d’un objet géométrique. Voici celles que j’utilise le plus :
- linecolor=couleur : permet de modifier la couleur du tracé. Il y a 19 couleurs prédéfinies sont : black, white, red, green, blue, cyan, magenta, yellow, lime, brown, darkgray, gray, lightgray, olive, orange, pink, purple, teal, violet. Par défaut linecolor=black. Pour les plus experts il est possible de définir ses propres couleurs par exemple en rgb avec la commande \newrgbcolor{ma_couleur}{165 209 82} pour le vert tilleul.
- linewidth=epaisseur : un nombre avec ou sans unité pour gérer l’épaisseur du trait. Par défaut linewidth=0.8pt. Le point typographique : 1pt=0,35mm ;
- linestyle=style : permet d’obtenir un trait plein, pointillé, tirets… Les différents styles sont : solid (trait plein), dashed (trait en tirets), dotted (trait en pointillés) et none (pas de trait). Pour dashed on peut ajouter l’option dash qui fixe la taille des tirets et l’espacement, par défaut dash=5pt 2pt. Pour dotted, dotsep permet de gérer l’espacement entre les points, dotsep=3pt par défaut.
- dotscale=facteur : permet de réduire ou d’agrandir la taille d’un point d’un coefficient facteur. Par défaut dotscale=1.
Exemples :
\begin{pspicture}(-5,-3)(5,3)
\psset{PointSymbol=+}
% Définition d'une nouvelle couleur en rgb, merci Gimp
\newrgbcolor{yeux_verts}{0.618 0.715 0.101}
\pstGeonode[PosAngle=-90](-4,-1){A}(-1,-2){B}
% Une épaisseur diminuée et une ligne orange
\pstLineAB[linewidth=0.4pt, linecolor=orange]{A}{B}
\pstGeonode[PosAngle=90](-2,2){C}(0,1){D}
% Usage de la couleur crée, épaisseur exprimée en millimètres
\pstLineAB[nodesepA=-1, linestyle=solid, linecolor=yeux_verts, linewidth=0.5mm]{C}{D}
\pstGeonode[PosAngle={90,-90}](1,-2){E}(3,-1){F}
% Ligne rouge en pointillés
\pstLineAB[nodesepB=-2, linestyle=dotted, linecolor=red]{E}{F}
% dotscale permet d'augmenter/diminuer la taille du point
\pstGeonode[PosAngle=60, dotscale=2, PointSymbol=*](-3,0){G}(2,1){H}
% ligne bleu épaisse en tirets, 10pt de long et 2pt entre chacun
\pstLineAB[nodesep=-1, linestyle=dashed, dash=10pt 2pt, linecolor=blue, linewidth=2pt]{G}{H}
\end{pspicture}
On peut aussi construire une droite passant par un point dont l’angle avec l’horizontal (axe des abscisses) est fixé.
\pstLineAA[Options]{A}{angle}{B}\pstLineAA[Options](x,y){angle}{B}
Créer un point B tel que la droite (AB) fasse un angle par rapport à l’axe des abscisses.
Exemples :
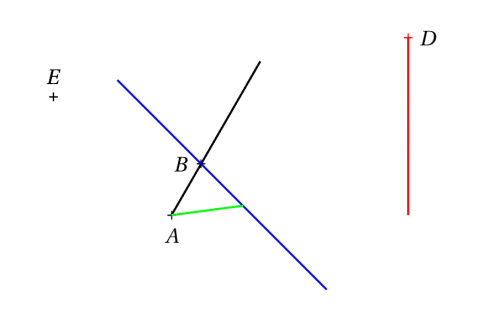
\begin{pspicture}(-5,-3)(5,3)
\psset{PointSymbol=+}
\pstGeonode[PosAngle=-90](-3,-2){A}
% Construire un point B tel que la droite (AB) soit inclinée de 60° par rapport à l'horizontale.
% On trace une demi-droite [AB)
\pstLineAA[PosAngle=180, nodesepB=-2]{A}{60}{B}
% Construire un point C tel que la droite (BC) soit inclinée de -45° par rapport à l'horizontale.
% On trace la droite (BC)
% Le point C n'apparaît pas mais il existe.
\pstLineAA[PointSymbol=none, PointName=none, nodesep=-2, linecolor=blue]{B}{-45}{C}
% Le point C existe, voici la preuve...
\pstLineAB[linecolor=green]{A}{C}
% Construire le point D tel que la droite passant par D et le point de coordonnées (1,0)
% forme un angle de 90° par rapport à l'horizontale.
\pstLineAA[nodesepA=-2, linecolor=red](1,0){90}{D}
% Placer un point E tel que la droite (AE) forme un angle de 135° avec l'horizontale
% On veut que E ait pour abscisse -5 et que la droite n'apparaisse pas.
% Voir ci-dessous pour \pstLineAbsNode
% Pour cela on utilise un point intermédiaire E'
\pstLineAA[linestyle=none, PointSymbol=none, PointName=none]{A}{135}{E'}
\pstLineAbsNode[PosAngle=90]{A}{E'}{-5}{E}
\end{pspicture}
Placer un point sur une droite
Voici quelques macros qui permettent de placer un point sur un droite :
\pstLineAbsNode[Options]{A}{B}{x}{C}
\pstLineOrdNode[Options]{A}{B}{y}{C}
Placer un point C sur la droite (AB) ayant pour abscisse (respectivement ordonnée) x (respectivement y).
Exemples :
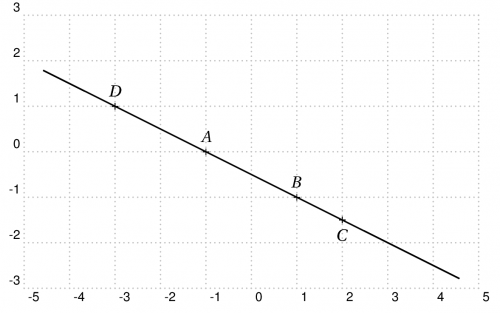
\begin{pspicture}[showgrid=true](-5,-3)(5,3)
\psset{PointSymbol=+}
\pstGeonode[PosAngle=90](-1,0){A}(1,-1){B}
% On trace une droite (AB)
\pstLineAB[nodesep=-4]{A}{B}
% Le point C se trouve sur la droite (AB), il a pour abscisse 2.
% C est crée comme avec \pstGeonode et les options sont les mêmes.
\pstLineAbsNode[PosAngle=-90]{A}{B}{2}{C}
% Le point D se trouve sur la droite (AB), il a pour ordonnée 1.
\pstLineOrdNode[PosAngle=90]{A}{B}{1}{D}
\end{pspicture}
On souhaite souvent placer un point sur une droite, une demi-droite ou un segment à une certaine distance d’une extrémité.
\pstLocateAB[Options]{A}{B}{distance}{C}
\pstExtendAB[Options]{A}{B}{distance}{C}
Créer sur le segment [AB] (respectivement sur la droite (AB) à l’extérieur de [AB]) un point C situé à la distance de A.
On ne peut pas indiquer une distance en unité de longueur usuelle. En effet la longueur à l’impression n’a pas forcément de lien avec les coordonnées choisies sur la figure. Pour faire référence à une distance il faut que deux points définissant cette distance soient crées. On utilise ensuite la commande :
\pstDist{A}{B}
Mesure la distance AB.
Exemples :
\begin{pspicture}(-5,-3)(5,3)
\psset{PointSymbol=+}
% On place A et B tel que AB=5
\pstGeonode[PosAngle=-90](-2,2){A}(3,2){B}
% On trace (AB) en magenta
\pstLineAB[nodesep=-3, linecolor=magenta]{A}{B}
% On définit E et F tel que EF=2, E et F sont invisibles.
% On ne peut pas faire passer une longueur, seulement une distance
% entre deux points crées.
\pstGeonode[PointName=none, PointSymbol=none](0,0){E}(2,0){F}
% On crée un point C sur [AB] tel que AC=EF
\pstLocateAB[PosAngle=90]{A}{B}{\pstDist{E}{F}}{C}
% On crée un point D sur [AB] tel que BC=EF
\pstLocateAB[PosAngle=90]{B}{A}{\pstDist{E}{F}}{D}
% On crée un point C' sur [AB) mais pas sur [AB] tel que BC'=EF
\pstExtendAB[PosAngle=90]{A}{B}{\pstDist{E}{F}}{C'}
% On crée un point D' sur [BA) mais pas sur [AB] tel que AD')EF
\pstExtendAB[PosAngle=90]{B}{A}{\pstDist{E}{F}}{D'}
\end{pspicture}
Milieu d’un segment, codage et étiquetage
\pstMiddleAB[Options]{A}{B}{I}
Crée le point I milieu du segment [AB]
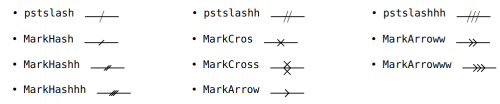
\pstSegmentMark[Options]{A}{B}
Ajoute un codage sur un segment.
Voici les codages disponibles
\pstLabelAB[Options]{A}{B}{etiquette}
Ajoute une étiquette au segment [AB].
Cette commande possède quelques options en plus des options habituelles vue ci-dessus (linewidth, linestyle…)
- arrows=symbole : pour obtenir des flèches ou autres par exemple pour des flèches aux extrémités : <->. Ou encore |-|, |<->|
- offset=distance : place l’étiquette à la distance offset du segment. La valeur est positive ou négative pour se placer au dessus ou en dessous du segment en fonction de l’orientation et de l’ordre des points.
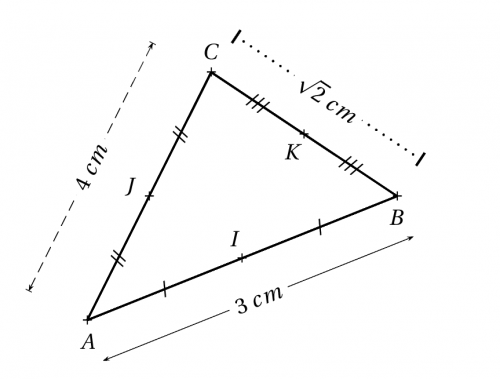
Exemples :
\begin{pspicture}(-5,-3)(5,3)
\psset{PointSymbol=+}
\pstGeonode[PosAngle={-90,-90,90}](-2,-1){A}(3,1){B}(0,3){C}
\pstLineAB{A}{B}
\pstLineAB{B}{C}
\pstLineAB{C}{A}
% On crée le milieu I de [AB], J de [AC] et K de [BC]
\pstMiddleAB{A}{B}{I}
\pstMiddleAB{A}{C}{J}
\pstMiddleAB{B}{C}{K}
% On code le milieu en marquant les segments [AI] et [IB]
\pstSegmentMark[SegmentSymbol=pstslash]{A}{I}
\pstSegmentMark[SegmentSymbol=pstslash]{I}{B}
% On ajoute la longueur du segment [AB] sous le segment à 20pt
\pstLabelAB[linewidth=0.2pt, linestyle=solid, arrows=<->,offset=-20pt]{A}{B}{$3~cm$}
% Codage différent des segments [AJ] et [JC]
\pstSegmentMark[SegmentSymbol=pstslashh]{A}{J}
\pstSegmentMark[SegmentSymbol=pstslashh]{J}{C}
% On ajoute la longueur du segment [AC] en modifiant la forme des flèches.
\pstLabelAB[linewidth=0.2pt, linestyle=dashed, arrows=|<->|,offset=30pt]{A}{C}{$4~cm$}
\pstSegmentMark[SegmentSymbol=pstslashhh]{B}{K}
\pstSegmentMark[SegmentSymbol=pstslashhh]{K}{C}
% On ajoute une longueur écrite en mode mathématique
\pstLabelAB[linewidth=1pt, linestyle=dotted, arrows=|-|,offset=20pt]{C}{B}{$\sqrt{2}~cm$}
\end{pspicture}
Cercle et arc de cercles
\pstCircleOA[Options]{O}{A}[angleA][angleB]
Tracer un cercle de centre O passant par A ou un cercle de rayon ou diamètre donné.
Deux options importantes :
- Radius=distance : trace un cercle de rayon distance où distance est la longueur d’un segment existant avec la commande \pstDistAB{A}{B} comme ci-dessus. Dans ce cas il faut laisser vide la seconde accolade.
- Diameter=distance : trace un cercle de diamètre distance où distance est du même type que ci-dessus. Il faut aussi laisser vide la seconde accolade.
- angleA=angle et angleB=angle : trace un arc de cercle depuis l’angleA jusque l’angle B dans le sens trigonométrique
\pstCircleAB[Options]{A}{B}[angleA][angleB]
Trace un cercle de diamètre [AB].
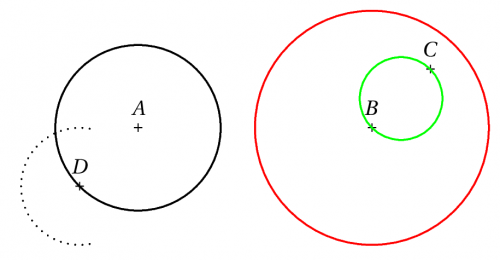
Exemples :
\begin{pspicture}(-5,-3)(5,3)
\psset{PointSymbol=+}
\pstGeonode[PosAngle=90](-2,0){A}(2,0){B}(3,1){C}(-3,-1){D}
\pstGeonode[PointSymbol=none, PointName=none](0,0){E}(2,0){F}
% Un cercle de centre A passant par D
\pstCircleOA{A}{D}
% Un cercle de diamètre [BC]
\pstCircleAB[linecolor=green]{B}{C}
% Un cercle de centre B et de rayon EF
\pstCircleOA[Radius=\pstDist{E}{F}, linecolor=red]{B}{}
% Un arc de cercle de centre D de diamètre EF entre 80° et 280
\pstCircleOA[Diameter=\pstDist{E}{F}, linestyle=dotted]{D}{}[80][280]
\end{pspicture}
Triangles
Bien que nous verrons plus tard des commandes pour définir des intersections, pst-eucl propose tout ce qu’il faut pour tracer et construire des triangles.
\pstTriangle[Options](x1,y1){A}(x2,y2){B}(x3,y3){C}
Définit trois points A, B et C et trace le triangle ABC.
\pstTriangleSSS[Options](pos){A}(a,b,c){B}{C}
Définit les points B et C tel que le triangle ABC aient pour mesures : BC=a, AC=b et AB=c.
- pos est facultatif. Il indique la position du point de départ par rapport au reste de la figure. Par défaut pos=L, left, A est à gauche de la figure. On peut choisir R (right), U (up) ou D (down).
C’est l’occasion de tracer le codage pour un angle droit :
\pstRightAngle[Options]{A}{B}{C}
L’option la plus utile est RightAngleSize=taille qui définit la taille du codage et vaut 0.28 par défaut
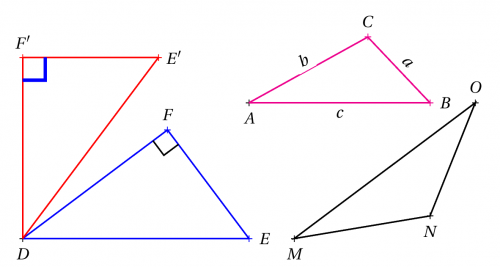
Exemples :
\begin{pspicture}(-5,-3)(5,3)
\psset{PointSymbol=+}
% Crée les points M, N et O et trace le triangle MNO
% Sans informations PosAngle les points sont placés au mieux
% PosAngle={90,90,90} ne fonctionne pas, il faut utiliser PosAngleA...
\pstTriangle[PosAngleA=-90, PosAngleB=-90, PosAngleC=90](1,-3){M}(4,-2.5){N}(5,0){O}
\pstGeonode[PosAngle=-90](0,0){A}(-5,-3){D}
% Trace le triangle ABC où BC=a=2, AC=b=3, AB=c=4
% Le point A est par défaut à gauche du triangle
\pstTriangleSSS[PosAngle={0,90}, linecolor=magenta]{A}(2,3,4){B}{C}
% Quelques étiquettes pour s'y retrouver
\pstLabelAB[offset=-7pt]{A}{B}{$c$}
\pstLabelAB[offset=7pt]{C}{B}{$a$}
\pstLabelAB[offset=7pt]{A}{C}{$b$}
% Trace le triangle DEF où EF=3, DF=4 et DE=5
% Le point D est à gauche du triangle
\pstTriangleSSS[PosAngle={0,90}, linecolor=blue]{D}(3,4,5){E}{F}
% On trace le codage de l'angle droit
\pstRightAngle{E}{F}{D}
% Trace le même triangle avec D en bas
\pstTriangleSSS[PosAngle={0,90}, linecolor=red](D){D}(3,4,5){E'}{F'}
% On trace le codage de l'angle droit en changeant quelques paramètres
\pstRightAngle[RightAngleSize=0.5, linecolor=blue, linewidth=2pt]{E'}{F'}{D}
\end{pspicture}
L’extension propose trois commandes de construction, les fameux cas d’égalité des triangles :
\pstTriangleSAS[Options](pos){A}(b,angleA,c){B}{C}
Trace un triangle ABC connaissant l’angle de sommet A et les deux côtés adjacents.
\pstTriangleASA[Options](pos){A}(angleA,c,angleB){B}{C}
Tracer un triangle ABC connaissant l’angle de sommet A, le longueur du segment AB=c et l’angle de sommet B, deux angles ayant un côté adjacent.
C’est l’occasion de présenter la commande de codage des angles :
\pstMarkAngle[Options]{A}{B}{C}{etiquette}
Marque l’angle de sommet $\widehat{ABC}$ avec étiquette.
Il y a quelques options intéressantes :
- MarkAngleRadius=rayon : rayon du marquage par défaut 0.4
- MarkAngleType=type : double ou triple pour doubler ou tripler l’arc
- Mark=marque : marquage de l’angle comme pour les segments MarkHash
- LabelSep=unité : 1 par défaut, permet de déplacer l’étiquette.
Exemples :
\begin{pspicture}(-5,-3)(5,5)
\psset{PointSymbol=+}
\pstGeonode[PosAngle=-90](0,0){A}
% Triangle ABC tel que l'angle de sommet A mesure 45°, AC=3 et AB=4
\pstTriangleSAS[PosAngle={-90,90}]{A}(3,45,4){B}{C}
% Marque l'angle de sommet A avec la mesure... attention au codage des degrés
\pstMarkAngle{B}{A}{C}{$45^{\circ}$}
% Triangle ADE tel que l'angle de sommet A mesure 60° et l'angle de sommet D mesure 30°
% AD=5
\pstTriangleASA[PosAngle={90,-90}](R){A}(60,5,30){D}{E}
% Double marquage de l'angle A
\pstMarkAngle[MarkAngleType=double]{D}{A}{E}{$60^{\circ}$}
% Triple marquage de l'angle D
\pstMarkAngle[MarkAngleType=triple, LabelSep=1.2]{E}{D}{A}{$30^{\circ}$}
\end{pspicture}
Polygone
Une commande pour tracer rapidement un polygone une fois que les points sont crées. C’est une commande pstricks qui utilise les points de pst-eucl comme des noeuds. On peut cependant utiliser l’option CurveType quand on crée les points en même temps.
\pspolygon[Options](A1)(A2)...(An)
Trace un polygone a n côtés
Exemples :
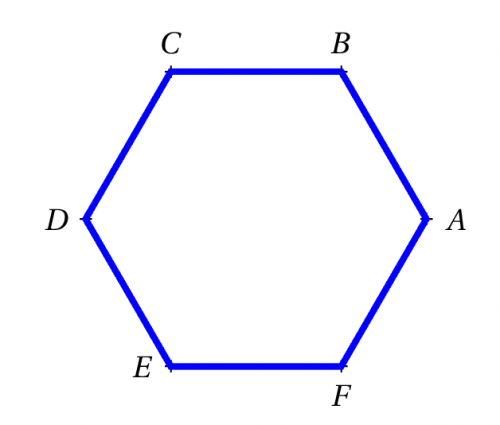
\begin{pspicture}(-5,3)(5,3)
\psset{PointSymbol=+}
% Les coordonnées polaires c'est pratique pour les polygones réguliers
\pstGeonode[PosAngle={0,90,90,180,180,-90,90}](2;0){A}(2;60){B}(2;120){C}(2;180){D}(2;240){E}(2;300){F}
% On trace le polygone
\pspolygon[linewidth=2pt, linecolor=blue](A)(B)(C)(D)(E)(F)
\end{pspicture}
Intersections de droites et de cercles
\pstInterLL[Options]{A}{B}{C}{D}{M}
Construit le point d’intersection M des droites (AB) et (CD).
Les options sont celles qui concernent le construction de points. Si les droites sont parallèles, le point ne se crée pas.
\pstInterLC[Options]{A}{B}{O}{C}{M}{N}
Construit les deux points d’intersection M et N entre la droite (AB) et le cercle de centre O passant par C.
Les options sont les options habituelles. Le rayon ou le diamètre du cercle peut être défini par Radius ou Diameter et \pstDist{A}{B} comme pour le tracé d’un cercle.
\pstInterCC[Options]{O1}{A}{O2}{B}{M}{N}
Construit les deux points d’intersection M et N des cercles de centre O1 passant par A et de centre 02 passant par B.
Les options sont les options habituelles. On peut fixer le rayon ou le diamètre de chaque cercle de la manière habituelle en utilisant les options RadiusA, DiameterA, RadiusB et DiameterB. On peut utiliser la collection de paramètres CodeFig pour afficher les traits de constructions (voir exemple).
Exemples :
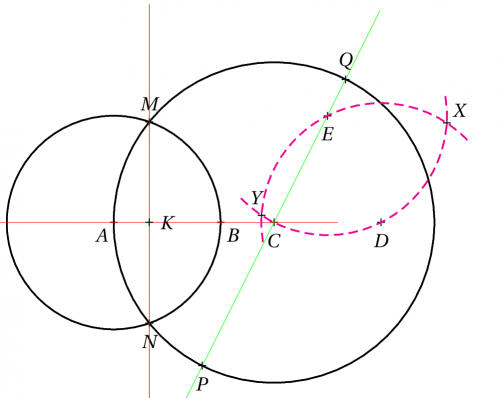
\begin{pspicture}(-5,-3)(5,3)
\psset{PointSymbol=+}
\pstGeonode[PosAngle={-135,-45,-90}](-2,0){A}(0,0){B}(1,0){C}(3,0){D}(2,2){E}
\pstCircleOA{A}{B}
\pstCircleOA{C}{A}
% M et N sont les intersections des cercles
% Par défaut les points sont crées mais pas affichés à l'écran
% Les paramètre PosAngleA et PosAngleB permettent l'affichage.
\pstInterCC[PosAngleA=90, PosAngleB=-90]{A}{B}{C}{A}{M}{N}
\pstLineAB[linecolor=red, nodesep=-2.2, linewidth=0.1pt]{A}{B}
\pstLineAB[linecolor=red, nodesep=-2.2, linewidth=0.1pt]{M}{N}
% K est le point d'intersection des droites (MN) et (BK)
\pstInterLL{M}{N}{A}{B}{K}
% P et Q sont les intersections des droites (CE) et du cercle de centre C passant par A
\pstLineAB[linecolor=green, nodesepA=-4.2, nodesepB=-2.2, linewidth=0.1pt]{C}{E}
\pstInterLC[PosAngleA=-90,PosAngleB=90]{C}{E}{C}{A}{P}{Q}
% Les paramètres CodeFig permettent de faire apparaître les traites de construction
% CodeFigA et CodeFigB servent à différencier les deux arcs
% CodeFigAarc est un booléen qui donne le sens trigonométrique ou non
\pstInterCC[CodeFigA=true, CodeFigB=true, CodeFigAarc=false, CodeFigBarc=true
CodeFigStyle=dashed, CodeFigColor=magenta, PosAngleA=45, PosAngleB=105]{E}{C}{D}{E}{X}{Y}
\end{pspicture}
Transformations géométriques
Les transformations usuelles du plan sont disponibles dans pst-eucl.
La symétrie axiale et projection orthogonale
\pstOrtSym[Options]{A}{B}{M1,M2...Mn}[M'1,M'2,...,M'n]
Construit les symétriques de M1,M2…Mn par la symétrie axiale d’axe (AB).
Par défaut les images sont codés en ajoutant une apostrophe, la partie entre crochet est ainsi facultative.
\pstProjection[Options]{A}{B}{M1,M2...Mn}[M'1,M'2,...,M'n]
Construit les projection orthogonale de M1,M2…Mn sur la droite (AB).
Exemples :
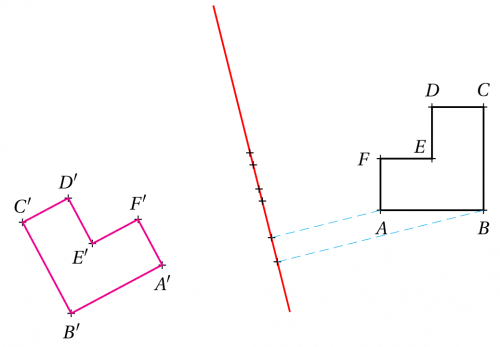
\begin{pspicture}(-6,-2)(6,4)
\psset{PointSymbol=+}
\pstGeonode[CurveType=polygon, PosAngle={-90,-90,90,90,135,180}](3,1){A}(5,1){B}(5,3){C}(4,3){D}(4,2){E}(3,2){F}
\pstGeonode[PointName=none, PointSymbol=none](1,0){X}(0,4){Y}
\pstLineAB[linecolor=red, nodesep=-1]{X}{Y}
% Une symétrie d'axe (XY)
\pstOrtSym[CurveType=polygon, linecolor=magenta,PosAngle={-90,-90,90,90,-135,90}]{X}{Y}{A,B,C,D,E,F}
% Des projections orthogonales
\pstProjection[PosAngle={180}, PointName=none]{X}{Y}{A,B,C,D,E,F}[A'',B'',C'',D'',E'',F'']
\pstLineAB[linecolor=cyan, linestyle=dashed, linewidth=0.1pt]{A}{A''}
\pstLineAB[linecolor=cyan, linestyle=dashed, linewidth=0.1pt]{B}{B''}
\end{pspicture}
La symétrie centrale
\pstSymO[Options]{O}{M1,M2...Mn}[M'1,M'2,...,M'n]
Construit les symétriques de M1,M2…Mn par la symétrie de centre O.
Par défaut les images sont codés en ajoutant une apostrophe, la partie entre crochet est ainsi facultative.
Exemples :
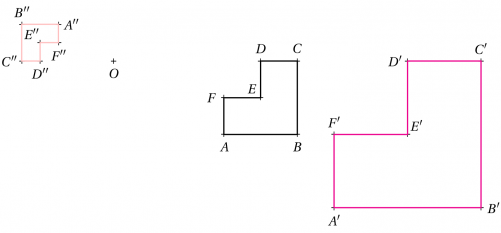
\begin{pspicture}(-6,-2)(6,4)
\psset{PointSymbol=+}
\pstGeonode[CurveType=polygon, PosAngle={-90,-90,90,90,135,180}](3,1){A}(5,1){B}(5,3){C}(4,3){D}(4,2){E}(3,2){F}
\pstGeonode[PosAngle=90](0,2){O}
% Une symétrie de centre O
\pstSymO[linecolor=blue, CurveType=polygon, PosAngle={90,90,-90,-90,135,0}]{O}{A,B,C,D,E,F}[A'',B'',C'',D'',E'',F'']
\end{pspicture}
La translation
\pstTranslation[Options]{A}{B}{M1,M2...Mn}[M'1,M'2,...,M'n]
Construit les symétriques de M1,M2…Mn par la translation qui transforme A en B.
Par défaut les images sont codés en ajoutant une apostrophe, la partie entre crochet est ainsi facultative.
Exemples :
\begin{pspicture}(6,4) \psset{PointSymbol=+} \pstGeonode[CurveType=polygon, PosAngle={-90,-90,90,90,135,180}](3,1){A}(5,1){B}(5,3){C}(4,3){D}(4,2){E}(3,2){F} \pstGeonode[PointSymbol=none, PosAngle=-90](1,4){U}(4,5){V} % Un peu de pstricks pour tracer un vecteur \psline[linewidth=2pt, linecolor=blue, arrows=->](U)(V) % Un translation de vecteur UV \pstTranslation[CurveType=polygon, linecolor=green, PosAngle={-90,-90,90,90,135,180}]{U}{V}{A,B,C,D,E,F} \end{pspicture}
La rotation
\pstRotation[Options, RotAngle]{O}{M1,M2...Mn}[M'1,M'2,...,M'n]
Construit les images de M1,M2…Mn par la rotation de centre O et d’angle direct RotAngle.
Par défaut les images sont codés en ajoutant une apostrophe, la partie entre crochet est ainsi facultative. L’option RotAngle=angle permet de définir l’angle dans le sens direct.
Exemples :
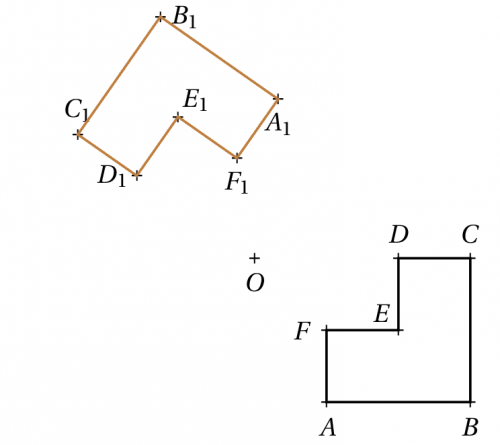
\begin{pspicture}(-2,0)(6,6)
\psset{PointSymbol=+}
\pstGeonode[CurveType=polygon, PosAngle={-90,-90,90,90,135,180}](3,1){A}(5,1){B}(5,3){C}(4,3){D}(4,2){E}(3,2){F}
\pstGeonode[PosAngle=-90](2,3){O}
% Une rotation de centre O et d'angle 145° dans le sens direct.
% J'utilise une notation avec indice
\pstRotation[linecolor=brown, CurveType=polygon, PosAngle={-90,0,90,180,45,-90}, RotAngle=145]{O}{A,B,C,D,E,F}[A1,B1,C1,D1,E1,F1]
\end{pspicture}
L’homothétie
\pstHomO[Options, HomCoef]{O}{M1,M2...Mn}[M'1,M'2,...,M'n]
Construit les images de M1,M2…Mn par l’homothétie de centre O et de coefficient HomCoef.
Par défaut les images sont codés en ajoutant une apostrophe, la partie entre crochet est ainsi facultative. L’option HomCoef=coef permet de définir le coefficient positif ou négatif de l’homothétie.
Exemples :
\begin{pspicture}(-2,0)(6,6)
\psset{PointSymbol=+}
\pstGeonode[CurveType=polygon, PosAngle={-90,-90,90,90,135,180}](3,1){A}(5,1){B}(5,3){C}(4,3){D}(4,2){E}(3,2){F}
\pstGeonode[PosAngle=-90](0,3){O}
% Une homothétie de rapport 2 et de centre O
\pstHomO[linecolor=magenta, CurveType=polygon,PosAngle={-90,0,90,180,45,90}, HomCoef=2]{O}{A,B,C,D,E,F}
% Une homothétie de rapport -0,5 et de centre O
\pstHomO[linecolor=pink, CurveType=polygon, PosAngle={0,90,180,-90,135,-90}, HomCoef=-0.5]{O}{A,B,C,D,E,F}[A'',B'',C'',D'',E'',F'']
\end{pspicture}
Parallèles et perpendiculaire
Construire la parallèle à une droite passant par un point
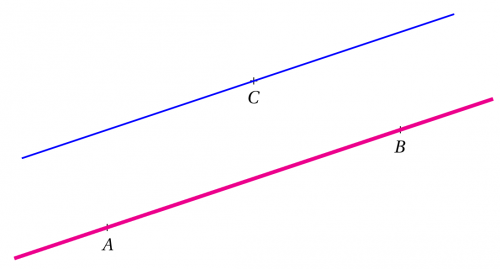
On veut construire la droite parallèle à la droite (AB) passant par C.
Il suffit de construire le translaté C’ de C dans la translation qui transforme A en B puis de tracer la droite (CC’).
\begin{pspicture}(-5,-3)(5,4)
\psset{PointSymbol=+}
\pstGeonode[PosAngle=-90](-3,-2){A}(3,0){B}(0,1){C}
\pstLineAB[nodesep=-2, linecolor=magenta, linewidth=2pt]{A}{B}
% On construit le translaté de C par la translation qui transforme A en B
% Le point C' n'est pas affiché
\pstTranslation[PointSymbol=none, PointName=none]{A}{B}{C}
\pstLineAB[nodesepA=-5, nodesepB=2,linecolor=blue]{C}{C'}
\end{pspicture}
Construire la perpendiculaire à une droite passant par un point extérieur à cette droite
On veut construire la droite perpendiculaire à la droite (AB) passant par C.
Il suffit de construire le projeté orthogonal C’ de C sur la droite (AB) puis de tracer (CC’)
\begin{pspicture}(-5,-3)(5,4) \psset{PointSymbol=+} \pstGeonode[PosAngle={-90,-90,0}](-3,-2){A}(3,0){B}(0,1){C} \pstLineAB[nodesep=-2, linecolor=magenta, linewidth=2pt]{A}{B} % On construit le projeté orthogonal C' de C sur (AB) \pstProjection[PointSymbol=none, PointName=none]{A}{B}{C} \pstLineAB[nodesepA=-1, nodesepB=-2,linecolor=blue]{C}{C'} % On construit le point d'intersection K de (AB) et de (CC') % pour pouvoir tracer l'angle droit. \pstInterLL[PointName=none, PointSymbol=none]{A}{B}{C}{C'}{K} \pstRightAngle{A}{K}{C} \end{pspicture}
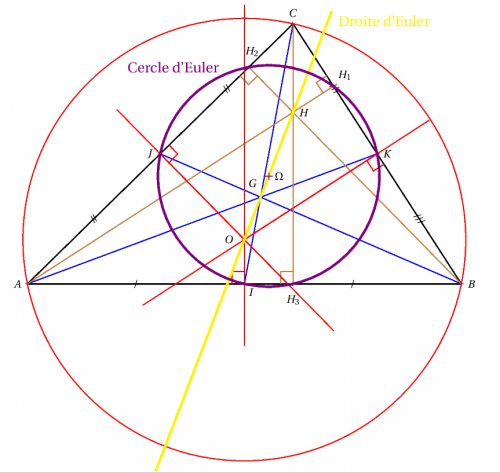
Un exemple complexe
\begin{pspicture}(14,14)
\psset{PointSymbol=+}
\pstGeonode[PosAngle=180](0,0){A}
% On trace un triangle ABC mesurant 10, 12 et 14
\pstTriangleSSS[PosAngle={0,90}]{A}(10,12,14){B}{C}
% On trace le milieu de I de [AB] et le codage
\pstMiddleAB[PosAngle=-50]{A}{B}{I}
\pstSegmentMark[SegmentSymbol=pstslash]{A}{I}
\pstSegmentMark[SegmentSymbol=pstslash]{B}{I}
% Le milieu J de [AC] et le codage
\pstMiddleAB[PosAngle=180]{A}{C}{J}
\pstSegmentMark[SegmentSymbol=pstslashh]{A}{J}
\pstSegmentMark[SegmentSymbol=pstslashh]{C}{J}
% Le milieu K de [BC] et le codage
\pstMiddleAB[PosAngle=0]{B}{C}{K}
\pstSegmentMark[SegmentSymbol=pstslashhh]{B}{K}
\pstSegmentMark[SegmentSymbol=pstslashhh]{C}{K}
% Tracé des médianes en bleu
\psset{linecolor=blue}
\pstLineAB{I}{C}
\pstLineAB{J}{B}
\pstLineAB{K}{A}
% Création du centre de gravité, on utilise une fonction spéciale
\pstCGravABC[PosAngle=120, PointNameSep=1.5em]{A}{B}{C}{G}
% Création des pieds des hauteurs
\pstProjection[PosAngle=45, PointNameSep=1.5em]{B}{C}{A}[H_1]
\pstProjection[PosAngle=80, PointNameSep=1.5em]{A}{C}{B}[H_2]
\pstProjection[PosAngle=-90, PointNameSep=1.5em]{A}{B}{C}[H_3]
% Tracé des hauteurs
\psset{linecolor=brown}
\pstLineAB{A}{H_1}
\pstLineAB{B}{H_2}
\pstLineAB{C}{H_3}
% Tracé des codages pour les perpendiculaires
\pstRightAngle{A}{H_3}{C}
\pstRightAngle{A}{H_2}{B}
\pstRightAngle{A}{H_1}{C}
% Création de l'orthocentre
\pstInterLL[PosAngle=0]{H_1}{A}{H_2}{B}{H}
% Tracé des médiatrices en rouge en utilisant une fonction spéciale
\psset{linecolor=red}
\pstMediatorAB[PointName=none, PointSymbol=none]{A}{B}{I}{I'}
\pstLineAB[nodesep=-2]{I}{I'}
\pstRightAngle{I'}{I}{A}
\pstMediatorAB[PointName=none, PointSymbol=none]{C}{A}{J}{J'}
\pstLineAB[nodesep=-2]{J}{J'}
\pstRightAngle{J'}{J}{C}
\pstMediatorAB[PointName=none, PointSymbol=none]{B}{C}{K}{K'}
\pstLineAB[nodesepA=-2, nodesepB=-4]{K}{K'}
\pstRightAngle{K'}{K}{B}
% Création du centre du cercle circonscrit en utilisant une fonction spéciale
\pstCircleABC[PosAngle=180, PointNameSep=1.5em]{A}{B}{C}{O}
% Tracé de la droite d'Euler en jaune
\psset{linecolor=yellow}
\pstLineAB[linewidth=2pt, nodesepA=-8, nodesepB=-3.5]{O}{H}
\rput(11.5,8.5){\Large \color{yellow}Droite d'Euler}
% Tracé du cercle d'Euler
\psset{linecolor=violet}
\pstCircleABC[PointName=\Omega, linewidth=2pt]{H_1}{H_2}{H_3}{Y}
\rput(4.7,7){\Large \color{violet}Cercle d'Euler}
\end{pspicture}
Commandes supplémentaires
\pstLineAS[Options]{A}{coefficient}{B}\pstLineAS[Options](x,y){coefficient{B}
Créer un point B tel que la droite (AB) (respectivement la droite passant par (x,y) et B) ait pour coefficient directeur le nombre coefficient.
\pstLineCoef[Options]{a,b,c}{A}{B}
Créer le point A et le point B tel que l’équation de la droite (AB) soit $ax+by+c=0$
\psDistABC{A}{B}{C}
Renvoie la distance entre le point C et la droite (AB).





























































Laisser un commentaire