Mise à jour du 30 juillet 2021 : il est conseillé de privilégier le code \( … \) pour entrer en mode mathématiques ligne dans LaTeX plutôt que $ … $. De même on préférera \[ … \] à $$ … $$ pour le mode hors ligne. Cet article a été écrit il y a un quelques temps et mes connaissances ont un peu progressé depuis !
Pourquoi utilise LaTeX au collège ?
Écrire des mathématiques sans LaTeX
Comment installer une distribution LaTeX ?
Installer un éditeur de texte pour LaTeX
Présentation du code LaTeX
Le minimum de LaTeX pour commencer
Écrire des mathématiques en LaTeX au collège, les bases
Un peu de géométrie en LaTeX avec Pstricks et pst-eucl
Pourquoi utiliser LaTeX au collège ?
LaTeX est un langage de composition de document crée dans les années 80. Il est beaucoup utilisé dans les milieux universitaires où il est la norme pour rédiger des documents scientifiques de qualité. On peut se demander alors pourquoi s’embêter à utiliser LaTeX au collège, ou dans le secondaire.
Les professeurs de mathématiques commencent souvent leur carrière en cherchant un outil de rédaction simple pour produire de joli document mathématique. L’image austère et universitaire de LaTeX font que ce merveilleux outil reste très minoritaire dans les établissements du secondaire. En tout cas après quelques années d’expérience dans ce domaine, je suis souvent resté le seul utilisateur de LaTeX et encore plus seul quand il s’agit d’utiliser LaTeX au collège.
Écrire des mathématiques sans LaTeX au collège
Il existe de nombreuses alternatives au LaTeX pour écrire des documents mathématiques. En voici une liste non exhaustive et non détaillée :
Libreoffice et son éditeur de mathématiques
Libreoffice et les macros Dmaths
Ma préférence va dans l’ordre à LyX puis Libreoffice, les logiciels libres et gratuits. Le dernier est un logiciel privatif et payant dont je n’ai pas de licence et pour lequel je suis incapable de vous donner le moindre conseil.
En dehors de ces remarques liés à la liberté, le reproche commun que je fais à ces outils est la lourdeur d’utilisation. Je ne supporte pas d’avoir à cliquer de nombreuses fois juste pour écrire le produit de deux fractions. Je préfère en général rester les mains sur le clavier quitte à taper quelques codes.
C’est la raison principale qui m’a inciter à utiliser le langage LaTeX pour rédiger mes documents, apprendre quelques codes simples pour accélérer ma saisie mathématiques. Je suis maintenant capable de rédiger directement en LaTeX une correction de sujet d’évaluation de mathématiques sans passer par le brouillon.
Enfin LaTeX est un investissement à long terme. Malgré son âge, LaTeX reste d’actualité, sans être complet voici quelques logiciels qui utilisent nativement LaTeX :
D’ailleurs comme nous sommes sous WordPress je ne résiste pas :
$latex \phi=\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+…}}}}=1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+…}}}}}\approx 1,61803399$
Comment installer un distribution LaTeX ?
Pour utiliser LaTeX au collège il faut distinguer deux instants :
- l’installation d’une distribution;
- l’installation d’un éditeur.
Installer une distribution LaTeX
L’expression distribution vient du monde Unix, il s’agit simplement d’un ensemble complet d’applications. En ce qui concerne LaTeX, une distribution est constitué de compilateurs (latex, pdftex, … ) de visualisateur (dvi, ps, pdf…), de polices de caractères, de modules pour étendre le langage ( mathématiques, musique, graphisme, … )
Il existe deux distributions LaTeX concurrentes pour Windows :
Peu familier du monde Windows, je fais le choix de TeXLive qui est la distribution habituelle sous Linux. Elle est aussi la distribution choisie dans l’indispensable $latex LaTeX$ par la pratique de Christian Rolland publié aux feu éditions O’Reilly. Vous allez le voir, installer cette distribution pour utiliser LaTeX au collège n’est pas si difficile.
Première étape : Téléchargement et décompression d’une image iso de DVD
Après plusieurs heures perdues avec l’installateur réseau de la TeXLive, j’insiste et je tente de graver une distribution sur DVD
- Aller sur le site TeXLive (il est en anglais ! );
- Choisir de télécharger une image iso de DVD sur ce serveur;
- Télécharger le fichier texlive2009.iso.xz environ 1,4 Go;
- Décompresser le fichier en utilisant xz, pou cela télécharger xzdec.exe;
- Placer xzdec.exe dans le même dossier que texlive2009.iso.xz;
- Lancer le shell de commande Windows, en tapant par exemple command dans exécuter ou rechercher;
- Se placer dans le dossier où se trouve les deux fichiers puis lancer xzdec.exe texlive2009.iso.xz >texlive.iso;
- Après un petit moment on obtient une image iso d’un peu plus de 3Go dans le dossier;
- Il n’y a plus qu’à utiliser votre logiciel de gravure préféré, en mode gravure d’image bien sur !
On peut aussi tester la clef usb plutôt qu’un dvd.
Seconde étape : Lancer l’installation
- Sur le disque lancer install-tl-advanced;
- Choisir les fichiers à installer, le Schéma GUTEnberg TeX Live scheme me semble approprié;
- Ne conserver que la langue française pour réduire l’installation;
- Puis Installer TeX Live (1335 MB);
- C’est long !! Près de 40 min ici !
Le compilateur et ses modules sont maintenant installés. Reste à installer un éditeur plus ou moins sophistiqué pour saisir et compiler nos documents.
Installer un éditeur pour LaTeX au collège
L’éditeur va permettre la saisie de vos documents en LaTeX. Il en existe de toutes sortes, certains presque totalement WYSIWYG (What You See Is What You Get) d’autres plus WYSIWYM (What You See Is What You Mean). Certains rudimentaires demandent une connaissance précise du langage, d’autres plus assistés. Pour utiliser LaTeX au collège, l’éditeur de texte est fondamental, il faut passer un peu de temps pour trouver l’outil adapté à ses besoins.
En voici une sélection :
- LyX
A ma connaissance le seul éditeur totalement WYSIWIG. Il est finalement très proche des traitements de texte classique.
Il existe en version Windows et Linux, ce qui est un avantage. C’est une solution simple pour débuter, et même pour la plupart des usages.
Il a les défauts de ses qualités, il est parfois plus long d’insérer une formule à la souris que de taper directement le code.
Ma seule frustration : il ne nécessite aucune connaissance en $latex LaTeX$ !!!! - TeXMaker
Un bon éditeur en version Linux et Windows.
Coloration syntaxique, indentation, compilation facile. Les principales commandes sont disponibles dans les menus. - TeXnicCenter
Une autre éditeur du même genre, mais seulement sous Windows et en anglais par défaut - TeXworks :
Bonne nouvelle, un éditeur fourni avec la TeXLive. Il a l’air pas mal, coloration syntaxique, indentation, compilation facile. Mais il faut connaître un minimum le langage pour commencer. - Vim
L’éditeur par excellence sous Linux, un bon éditeur sous Windows ( désolé pour les amateurs de emacs, ce n’est pas un troll !).
Vim n’est pas dédié à $latex LaTeX$ mais il s’y adapte facilement.
C’est évidemment une solution à réserver aux amateurs de ligne de commande, de sobriété… et donc de rapidité…
C’est le choix que j’ai fait pour moi… et que je déconseille largement !
Présentation du code LaTeX
Un fichier LaTeX est un simple fichier texte, on peut le lire avec n’importe quel éditeur (notepad, vim, éditeurs spécialisés..). Avant de vous servir de LaTeX au collège il faut être au clair avec la structure suivante :
Le code est constitué de deux parties :
- le préambule : il indique le type de document, les modules à utiliser, les macros commandes, …
- le corps du document.
Voici un exemple simple qui produit à peu près ceci :
Vive les racines carrées : $latex \sqrt{5}$
Préambule
| documentclass{article} | Tous les fichiers LaTeX commencent par la déclaration du type de document, ici un article |
| usepackage[frenc]{babel}
renewcommand{R}{sqrt} |
Liste des packages nécessaire à la compilation du fichier, ici les règles de la typographie française
Une déclaration de macro, celle-ci remplace /sqrt par /R pour la racine carrée. |
Corps du document
| begin{document}
Vive les racines carrées : $\sqrt{5}$ end{document} |
Le corps du document
Les formules mathématiques sont encadrés par les symboles $ … $ |
Le type de document
Le choix d’une classe de document détermine la structure de celui-ci.
La classe que j’utilise principalement est article, elle offre un découpage en divisions que voici :
- Partie : part
- Chapitre : chapter
- Section : section
- Sous-section : subsection
- Sous-sous-section : subsubsection
- Paragraphe : paragraph
- Sous-paragraphe : subparagraph
La classe book utilise les mêmes divisions avec des différences de pagination. Il existe aussi une classe report dans le même genre.
D’autres existent, comme letter ou beamer (pour faire des diaporamas ! )… et vous pouvez même construire la votre !
Pour un usage quotidien, la classe article me semble la plus généraliste.
Signalons enfin que de nombreuses options de classe existent, par exemple :
documentclass[10pt,a4paper,landscape,]{article} : 10pt indique la taille de la police normale pour tout le document (11pt et 12pt sont disponibles)
Mon préambule
La liste des packages ou modules à utiliser est difficilement exhaustive. Tim Toady comme on dit en Perl ( There Is More One Way To Do It ).
Voici ceux que j’utilise :
usepackage[utf8]{inputenc} : Je suis sous Linux et j’utilise l’encodage utf8, mettre Latin1 sous Windows
usepackage[T1]{fontenc} : Pour avoir des caractère accentué.
usepackage{amsmath} : Un module de l’American Mathematical Society pour par exemple mettre beau chapeau sur les angles
usepackage{amsfonts} : Idem
usepackage{amssymb} : Idem
usepackage{geometry} : Gestion des marges du document, voir plus bas
usepackage{eurosym} : Le symbole euro
usepackage{pstricks} : La géniale boite à outils pour dessiner en postscript
usepackage{tikz} : Une autre manière de dessiner orienté pgf
usepackage{multicol} : Gestion du passage à plusieurs colonnes sur une page
usepackage{lscape} : Pour passer en mode paysage sur une page et pas sur d’autre
usepackage{graphics} : Insertion d’image
usepackage{array} : Une gestion des tableaux plus élaborée
usepackage{mathpazo} : Une jolie police pour les formules mathématiques
usepackage{makeidx} : Pour faire des index
usepackage[francais]{babel} : La typographie française sans soucis
Cette liste en plus d’être non exhaustive est en perpétuelle évolution, en fonction de mes besoins.
Mon préambule est à votre disposition.
J’ai rajouté dans mon préambule un pagestyle{empty} qui évite la numérotation des pages, un pagestyle{plain} permet de le rétablir.
On peut remarquer aussi l’usage du package géometry qui permet de gérer les marges du documents avec la déclaration suivante :
| geometry{ | ||
| a4paper, | Le type de papier | |
| tmargin=1cm, | La marge en haut | |
| bmargin, | La marge en bas | |
| rmargin=1cm, | La marge à droite | |
| lmargin, | La marge gauche | |
| headheight=0cm, | L’entête | |
| footskip, | Le pied de page | |
| } |
Et voilà… il est un peu tôt pour parler de macros.
Le corps du document
Il commence à begin{document} et s’achève à end{document}.
Et c’est là que se trouve l’essentiel, non ?
LaTeX au collège et le minimum de traitement de texte
Cette partie montre comment utiliser les commandes basiques de LaTeX au collège, par exemple :
- mettre en gras, en italique;
- changer la taille des caractères;
- centrer, aligner à droite…
Le minimum pour survivre
Les commandes commencent par le caractère (anti-slash)
Un passage à la ligne n’est pas interprété comme tel par LaTeX, il faut laisser une ligne vierge pour changer de paragraphe.Pour forcer un passage à la ligne on peut utiliser, mais c’est rare, \ .
On utilise souvent les accolades {… } pour délimiter un bloc de texte, par exemple pour changer la taille de la police :
Taille normale {Huge ceci est en énorme} et retour à la normal.
Les accolades peuvent bien sur être imbriquées.
De nombreuses commandes se présentent sous la forme :
begin{commande}
…
end{commande}
Le caractère % permet de commenter le fichier.
Le caractère ~ permet d’indiquer qu’un espace est insécable ( pas de passage à la ligne )
La taille des caractères
En typographie classique, on mesure la taille des caractères en point. 1pt=0,03515cm.
Dans la déclaration initiale documentclass[10pt]{article} on indique la taille, 10pt, du style normal dans tout le document. On a le choix entre 10pt (par défaut) , 11pt et 12pt.
Il y a alors 10 tailles de caractères possibles :
| 10pt | 11pt | 12pt | |
| /Huge | 25pt | 25pt | 25pt |
| /huge | 20pt | 20pt | 25pt |
| /LARGE | 18pt | 18pt | 20pt |
| /Large | 14pt | 14pt | 18pt |
| /large | 12pt | 12pt | 14pt |
| /normalsize | 10pt | 11pt | 12pt |
| /small | 9pt | 10pt | 11pt |
| /footnotesize | 8pt | 9pt | 10pt |
| /scriptsize | 7pt | 8pt | 8pt |
| /tiny | 5pt | 6pt | 6pt |
Il suffit d’écrire {Huge Voici un texte en énorme} pour changer de taille de caractère.
Le style des caractères
Mettre en gras, en italique, en penché… et bien plus encore !
| textnormal{texte} | pour écrire en caractères normaux (par défaut) donc inutile ! |
| textit{texte} | pour écrire en caractères italiques. |
| textsl{texte} | pour écrire en caractères penchés. |
| textbf{texte} | pour écrire en caractères gras. |
| texttt{texte} | pour écrire en caractères machine à écrire. |
| textsf{texte} | pour écrire en caractères linéaux. |
| textsc{texte} | pour écrire en petites capitales. |
On peut mélanger, bien sûr, même si je n’ai jamais compris à quoi servait un texte écrit en gras et en italique !!
Attention, il n’existe pas de petites capitales grasses.
Les dispositions de texte classiques
Centrer
On peut utiliser l’environnement center pour un paragraphe entier ou la commande centerline pour une seule ligne :
begin{center}
Tout ce texte sera centré
Ce paragraphe aussi
Et même celui-la\
Avec un saut de ligne forcé
end{center}
Ou pour une seule ligne :
centerline{Huge Je veux centrer ce truc énorme }
Tout à gauche, sans justification
C’est l’environnement flushleft.
begin{flushleft}
…
end{flushleft}
Tout à droite
C’est l’environnement flushright.
begin{flushright}
…
end{flushright}
Les espacements verticaux et horizontaux
Quand on souhaite marquer des sauts de lignes plus importants, on dispose des commandes suivantes :
| vspace{1cm} | Espace vertical de 1cm |
| hspace{1cm} | Espace horizontal de 1cm |
| bigskip | Espace vertical important et proportionnel à la police de base |
| medskip | Espace vertical moyen et proportionnel à la police de base |
| smallskip | Espace vertical petit et proportionnel à la police de base |
| vfill | Espace vertical déterminé en fonction de la place sur la page |
| hfill | Espace horizontal déterminé en fonction de la place sur la ligne |
Un exemple pour finir
Voici le résultat, et ci-dessous le code source.
documentclass[10pt]{article}
usepackage[utf8]{inputenc}
usepackage[T1]{fontenc}
usepackage{geometry}
usepackage[francais]{babel}
pagestyle{empty}geometry{
a4paper, % a4
tmargin=2cm, % Marge haute
bmargin=2cm, % Marge basse
lmargin=2cm, % Marge gauche
rmargin=2cm, % Marge droite
headheight=0cm, % Entete
headsep=0cm, % Séparateur entete
footskip=0cm % Pied de page
}
begin{document}
centerline{Huge Voici le titre en Huge}
vspace{2cm}
textit{Un exemple en italique}, puis un texte normal, textbf{Large un peu de gras et Large}, textsc{des petites capitales en taille normale}.
bigskip
On peut écrire un texte à partir de la marge gauche et la suite hspace{4cm} 4cm plus loin.
Ou encore
Écrire un texte hfill et la suite le plus loin possible sur la même ligne
vspace{3cm}
Nous voici 3cm plus bas !
begin{flushright}
Ce texte en taille normale est à droite…
texttt{Celui-ci en machine à écrire aussi}
{scriptsize Quelques mots en plus petit}
end{flushright}
vspace{1cm}
begin{center}
Nous sommes centré et 1cm plus bas !
Un peu de hfill texte centré mais loin…\
Centré
smallskip
{tiny Tout petit et centré}
vfill
Nous prenons toute la place verticale.
On va se retrouver en bas de la page…
{tiny} Même en tout petit, et centré
{LARGE Gros mais centré}
end{center}
end{document}
Il est grand temps de faire des maths. Non ?
Le minimum de mathématiques pour utiliser LaTeX au collège
Voici l’essentiel des expressions mathématiques utilisées au collège et leurs traduction LaTeX.
En LaTeX, on passe en mode mathématiques par le balisage $ … $ ou $$ … $$ pour la mise hors-ligne.
Sachant que WordPress accepte le code LaTeX à travers le balisage $ latex code LaTeX$, le tableau suivant est doublement utile.
| Expression mathématique | Expression en LaTeX |
|---|---|
| $latex 10-4+6\times 2 \div 3=10$ | $10-4+6\times 2 \div 3=10$ |
| $latex \dfrac{1}{3}-\dfrac{\dfrac{1}{4}}{1-\dfrac{1}{4}}$ | $\dfrac{1}{3}-\dfrac{\dfrac{1}{4}}{1-\dfrac{1}{4}}$
Mode hors-texte ou displaystyle |
| $latex \frac{1}{3}-\frac{\frac{1}{4}}{1-\frac{1}{4}}$ | $\frac{1}{3}-\frac{\frac{1}{4}}{1-\frac{1}{4}}$
Mode en ligne pour intégrer la formule dans une phrase |
| $latex \dfrac{4}{3} \approx 1,333$ à $latex 10^{-3}$ près | $\dfrac{4}{3} \approx 1,333$ à $10^{-3}$ près |
| $latex x \leqslant \pi$ et $latex y \geqslant \phi$ | $x \leqslant pi$ et $y \geqslant phi$ |
| $latex 10^{2^3+3^2}=10^{17}$ | $ 10^{2^3+3^2}=10^{17}$ |
| $latex \sqrt{5+7} \neq \sqrt{5} + \sqrt{7}$ | $ \sqrt{5+7} \neq \sqrt{5} + \sqrt{7}$ |
| $latex (x+2)^2=x^2+2x+4$ | $(x+2)^2=x^2+2x+4$ |
| $latex \left (\dfrac{x+2}{x-2}\right )^2$ | $\left (\dfrac{x+2}{x-2}\right )^2$ |
| $latex \left [\left(\dfrac{x}{2}+3 \right)-(x-4) \right]$ | $\left [\left(\dfrac{x}{2}+3 \right)-(x-4) \right]$ |
| $latex A \in [AB]$ et $latex A \notin ]AB)$ | $A \in [AB]$ et $A \notin ]AB)$ |
| $latex \widehat{ABC}=45^{\circ}$ | Solution pour WordPress :
$\widehat{ABC}=45^{\circ}$ Solution plus classique (package inputenc): $\widehat{ABC}=45\mathdegree$ |
| $latex \widehat{ACB}$ intercepte l’arc $latex \overset{\frown}{AB}$ | $\widehat{ACB}$ intercepte l’arc $\overset{\frown}{AB}$ |
| $latex \left \lbrace \begin{array}{l}2x+3y=7\ 3x-5y=9 \end{array} \right.$ | $\left \lbrace \begin{array}{l}2x+3y=7\ 3x-5y=9 \end{array} \right.$ |
| $latex \underbrace{2x+1}_{Premier membre}=\underbrace{3x-7}_{Second membre}$ | $\underbrace{2x+1}_{Premier membre}=\underbrace{3x-7}_{Second membre}$ |
C’est facile, non !
$latex \phi=\sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+…}}}}=1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{1+…}}}}}\approx 1,61803399$
Un peu de géométrie dans nos fichiers LaTeX au collège
Pstricks est une suite de macro-commandes pour insérer des figures PostScript directement dans un fichier LaTeX. C’est un des moyens les plus élégants et efficaces pour obtenir des figures de grandes qualité.
Avant de se lancer dans du vrai pstricks à écrire à la main, je vous signale que Geogebra sait exporter ses figure en pstricks. C’est une excellent alternative au codage manuel. On fait une jolie figure puis on insère le code dans son fichier source… et hop …
Les bases de l’extension pstricks pour LaTeX au collège
Pour intégrer une figure géométrique à un document, la méthode classique consiste à produire la figure avec le logiciel de notre choix puis de l’intégrer dans notre document sous forme d’objet graphique. $latex LaTeX$ permet bien sûr cette manipulation basique. Je vous propose cependant ici d’intégrer une figure sous forme de code directement dans le document. L’avantage principal étant pour moi l’indépendance du fichier : il contient à lui seul texte et figure.
PSTricks est un outils développé pour cela. Cette extension utilise les fonctions de PostScript pour fournir des commandes de dessin.
Pour mémoire PostScript est un langage inventé par Adobe pour décrire une page graphique. Il est compris directement par la plupart des imprimantes ce qui préserve des modifications à l’impression et garantie de manière extrêmement rigoureuse la dimension des objets imprimés. ( Tout le monde sait que les profs de math n’aiment pas que l’on mesure les figures photocopiées … )
PSTricks est une extension de $latex LaTeX$ qui offre les possibilités classiques du dessin vectoriel ( segment, polygone, cercle, courbes de Bézier ). Elle possède des modules supplémentaires dédiés à la 3D (pst-3d ), à la couleur (pst-fill, pst-grad ), au tracé de fonctions mathématiques (pst-plot)… Pour le prof de math, le module pst-eucl est incomparable : il permet des constructions géométriques euclidiennes à la manière des logiciels de géométrie comme Cabri ou Drgeo.
Voici la page officiel où vous trouverez davantages d’informations : http://tug.org/PSTricks/
Utiliser PSTricks dans un document $latex LaTeX$ est assez simple.
Il faut déclarer l’usage de l’extension :
usepackage{pstricks}
Puis pour dessiner on utilise une nouvel environnement :
begin{pspicture}[Options][Ligne de Base]($latex x_0,y_0$)($latex x_1,y_1$)
…
Un joli dessin
…
end{pspicture}
Les commandes entre crochets sont optionnelles.
La commande Options par exemple permet de fixer des paramètres comme : linestyle=dotted, linewidth=0.3 etc…
Le paramètre ($latex x_0,y_0$) est fixé à (0,0) s’il est absent. Ce sont les coordonnées du coin inférieur gauche de la figure. Le paramètre obligatoire ($latex x_1,y_1$) correspond aux coordonnées du coin supérieur droit.
Une version étoilée ( pspicture* ) existe : elle n’imprime pas les parties du dessin qui sortent de la boite.
Comme on le comprend, la figure se construit dans un repère orthonormé dont on fixe les limites au départ. Il faut ensuite décrire chaque objet par ses coordonnées.
Pour conclure ce premier billet dessinons un triangle :
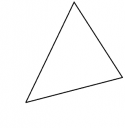
begin{pspicture}(5,5)
psline(1,1)(5,2)(3,5)(1,1)
end{pspicture}
Remarquons que dans la déclaration de l’environnement je n’ai fait référence qu’au bord supérieur droit, le bord inférieur gauche est donc à (0,0).
La commande psline permet de tracer un segment joignant des points dont on donne les coordonnées. Facile non ?
Cette commande, et toutes les autres, ont en commun d’avoir de nombreuses options supplémentaires qui permettent de modifier le style des segments ( pointillées, épaisseur, des flèches aux extrémités … )
Utiliser l’extension pst-eucl dans LaTeX au collège
Comme LaTeX au collège, de nombreuses extensions sont disponibles pour la plupart des situations. Pour mes cours au collège, j’utilise souvent pst-eucl, par Dominique Rodriguez. C’est un équivalent de Geogebra, mais en ligne de commande. On définit les points de départ, puis on utilise des commandes du type, milieu, médiatrice, bissectrice… Je vous renvoie à la documentation pour vous faire une idée.
Voici un exemple que j’utilise en cinquième. Une figure de départ et c’est pst-eucl qui se charge de faire les symétries centrales et axiales.
—
Ajouter cette ligne dans le préambule du fichier tex
usepackage{pstricks, pst-eucl}
Puis
—
begin{pspicture}(24,16) psset{PointSymbol=+} pstGeonode[PosAngle={-90,-90,270,-45,45,45,90,45,-45,235}, CurveType=polygon](5,3){A}(8,3){B}(11,5){C}(11,8){D}(8,8){E}(8,11){F}(5,8){G}(2,8){H}(2,5){I}(5,5){J} pstGeonode[PointSymbol=none, PointName=none](16,15){D_1}(10,0){D_2} pstGeonode[dotsize=4pt, PosAngle=90](12,10){O}pstLineAB[nodesep=-10]{D_1}{D_2} pstOrtSym[CurveType=polygon]{D_1}{D_2}{A,B,C,D,E,F,G,H,I,J}[A’,B’,C’,D’,E’,F’,G’,H’,I’,J’] pstSymO[CurveType=polygon]{O}{A,B,C,D,E,F,G,H,I,J}[A »,B »,C »,D »,E »,F »,G »,H »,I »,J »] end{pspicture}
—
psset permet de faire passer des options, comme PointSymbol que je préfère en + plutôt que x ou *.
La ligne pstGeonode permet de définir les points par leurs coordonnées, l’argument PosAngle indique la position du nom du sommet par rapport au point, l’argument CurveType permet de joindre les points.
Je définis une droite par deux points invisibles D_1 et D_2 et un centre de symétrie O
pstOrtSym et pstSymO terminent le boulot.
Je peux affirmer aux élèves que c’est bien l’ordinateur qui a produit le calque de correction !
J’espère que cet article vous aura convaincu qu’utiliser LaTeX au collège n’était pas une folie de geek. La qualité des documents obtenus, leur portabilité et pérennité devrait nous inciter à regarder comment se servir efficacement LaTeX au collège.
















Laisser un commentaire