Mise à jour du 2 janvier 2019
À faire :
- travailler la partie histoire (maths égyptiennes, grecques, indiennes, arabes et modernes)
- refondre avec l’article sur les fractions au cycle 3
- ajouter mes contrôles et fiches de synthèse
Dans cet article je me propose de collecter toutes les informations pédagogiques utiles à l’enseignement des fractions au collège pour le cycle 3 (sixième) et le cycle 4 (cinquième, quatrième et troisième). Pour rester dans le champ de mes compétences professionnelles, je n’aborderai pas les sujet des fractions à l’école primaire même si les éléments mathématiques présentés ici sont très largement utiles pour le cycle 3.
Ressources à utiliser en classe
Au cycle 3
Au cycle 4
Quelques éléments de connaissances pour le prof et les élèves
Voici quelques éléments de cours pour les élèves du cycle 4 et du cycle 3. J’ajoute de nombreuses démonstrations sous forme d’exemples génériques. La plupart des ces raisonnements ne peuvent pas être conduits en classe ni même être écrit dans un cahier de mathématiques de collégien. Cependant il me semble utile d’avoir les idées claires sur certains de ces sujets qui de prime abord paraissent évident mais qui demandent néanmoins d’avoir envisagé au préalable les obstacles mathématiques qui deviendront les obstacles didactiques à faire franchir aux élèves.
Dans un premier temps voici les connaissances brutes à mettre en place tout au long du collège. Je proposerai ensuite une progression sur l’ensemble du cycle 4 conforme aux programmes et aux repères de progression.
De la fraction partage à la fraction quotient
Il s’agit d’une problématique de cycle 3 qui consiste à passer de la notation $\frac{3}{4}$ définie comme trois parts parmi quatre à la fraction quotient où $\frac{3}{4}$ devient le nombre qui multiplié par $4$ est exactement égal à $3$.
En tant que nombre, on peut présenter les fractions comme des compléments des nombres ordinaires. Plus précisément, sachant connu l’arithmétique sur les nombres entiers on cherche à construire de nouveaux nombres permettant de compléter des égalités du type :
$7 \times ?=9$
La fraction quotient $displaystyle \frac{9}{7}$ va remplir ce rôle et l’argumentation qui suit souhaite montrer comment construire des opérations sur les fractions en partant de cette définition initiale. Cette manière de construire les fractions est assez proche de la construction moderne des nombres rationnels en partant de l’anneau des nombres relatifs : elle consiste à créer les nombres rationnels en construisant le corps des fractions $\mathbb{Q}$ de l’anneau intègre $\mathbb{Z}$.
Définition
$a$ et $b$ des entiers relatifs avec $b \neq 0$
On définit le nombre $\frac{a}{b}$ comme le nombre vérifiant l’égalité suivante :
$\displaystyle b \times \frac{a}{b}=a$
La fraction définie de cette manière correspond donc au quotient de $a$ par $b$.
$a$ est le numérateur de la fraction, $b$ est son dénominateur.
Remarques :
En fin de cycle 3, cette manière de définir la fraction permet d’ajouter de nouveaux nombres aux nombres entiers et décimaux déjà découverts à l’école primaire. Même si il est recommandé de commencer par présenter les fractions décimales avant les nombres à virgule, il faut bien avouer que leurs présences dans le quotidien fait que la plupart des enfants ont été en contact avec « les nombres à virgule » avant la définition de la fraction comme quotient en fin de cycle 3.
Ainsi on peut proposer de compléter quelques opérations à trou pendant la mise en place de cette nouvelle notion, en veillant à proposer des solutions entières, décimales mais aussi non décimales.
On évite en pratique les dénominateurs négatifs. En utilisant la propriété sur la division des relatifs on peut obtenir des écritures plus habituelles :
$\displaystyle \frac{5}{-3}=\frac{-5}{3}=-\frac{5}{3}$
$\displaystyle \frac{-5}{-3}=\frac{5}{3}$
Il est souvent plus pratique d’avoir le signe au numérateur ou devant la fraction.
Exemples
$7 \times ~~~~ = 56$ on teste les tables de multiplication ! $\displaystyle \frac{56}{7}=8$
$6 \times ~~~~ =9$ la réponse $1,5$ est possible, $\displaystyle \frac{9}{6}=1,5$
$10 \times ~~~~=5$ on attend la réponse $\displaystyle 0,5=\frac{5}{10}$
$3 \times ~~~~=10$ ici aucune réponse ne vient avant la définition $\displaystyle \frac{10}{3}$
Dans ce dernier cas un travail peut être mené avec la réponse $3,33$ ou $3,33333$.
On montre l’insuffisance des nombres décimaux pour compléter ces multiplications à trou.
$3,33333 \times 3=9,99999$ et quelque soit la précision on atteint jamais $10$.
Il faudra aussi discuter de l’écriture $3,3333…$ et demander le sens qu’elle peut avoir. Il est utile de préciser qu’un nombre décimal est une fractions décimale, c’est à dire une fraction dont le numérateur est un nombre entier et le dénominateur une puissance de 10. L’écriture $3,3333…$ n’est donc pas une écriture décimale à la différence de $\displaystyle 3,333~333=\frac{3~333~333}{10~000~000}$
Il revient au même de dire qu’un nombre décimal est un nombre que l’on peut écrire en utilisant les 10 chiffres (0; 1; … ; 9) de notre système décimal. De cette manière les nombres entiers sont décimaux car on peut les écrire $\displaystyle 2~018=\frac{2~018}{1}$, les nombres à virgule ayant un nombre fini de chiffre aussi !
La démonstration de l’existence et de l’unicité des nombres rationnels ne relève pas des connaissances du secondaire. Ils sont une conséquence de la construction du corps des rationnels comme complément de l’anneau des entiers relatifs. La construction des inverses permet d’obtenir le corps des rationnels et donc l’existences de ces nombres. La relation d’équivalence introduite sur les couples de nombres entiers relatifs permet d’obtenir ensuite l’unicité.
Comme $0 \times a=0$ pour tout nombre entier relatif $a$ cette égalité n’a de sens que pour $a=0$.
Dans un premier temps cela permet d’éliminer les écritures du type $\displaystyle \frac{a}{0}$ qui n’ont aucun sens pour $a\neq 0$.
Il semble alors que le nombre $\displaystyle \frac{0}{0}$ ait une existence comme nombre vérifiant $0 \times \frac{0}{0}=0$.
Cependant comme cette égalité est vraie pour tout nombre réel $x$, $0 \times x=0$ l’écriture $\displaystyle \frac{0}{0}$ correspondrait ainsi à une infinité de nombres, et même à tous les nombres, ce qui lui retire son intérêt et l’unicité !
Fraction d’une quantité
Une question difficile est la justification de l’affirmation selon laquelle « prendre une fraction d’une quantité revient à multiplier cette quantité par la fraction ». C’est la notion de fraction comme opérateur que l’on retrouve dans des énoncés du type :
- les 7 tiers de 13 ;
- 70 pourcent de 50 euros.
On peut lire avec intérêt à ce sujet un document ancien d’accompagnement des programmes de 2008.
Première étape : le tiers de 13 et 13 fois un tiers
Montrons dans un premier temps que le tiers de $13$ est égal à $13$ fois un tiers.
On sait que $\displaystyle 3 \times \frac{1}{3}=1$
En multipliant cette égalité par $13$ on arrive à :
$\displaystyle 13 \times 3 \times \frac{1}{3}=13 \times 1$
$\displaystyle 3 \times 13 \times \frac{1}{3}=13$
Or on sait que $\displaystyle 3 \times \frac{13}{3}=13$ on en déduit que :
$\displaystyle 13 \times \frac{1}{3}=\frac{13}{3}$
À partir de cet exemple générique on montre ainsi que :
Propriété
Pour $a$ et $b$ deux entiers et $b \neq 0$ on a :
$\displaystyle a \times \frac{1}{b}=\frac{a}{b}$
Remarque :
On est pas loin d’avoir montré que diviser par $b$ revient à multiplier par son inverse $\displaystyle \frac{1}{b}$, mais nous reviendrons plus tard sur cette idée.
Deuxième étape : 7 tiers de 13 et 7 fois 13 tiers
7 tiers de 13 revient à calculer 7 fois le tiers de 13.
Nous venons de voir que le tiers de 13 correspond au nombre $\displaystyle \frac{13}{3}$
Ainsi l’expression 7 tiers de 13 renvoit à $7\displaystyle \times \frac{13}{3}$ et non pas $\displaystyle \frac{7}{3} \times 13$
Cependant en revenant à la définition, $\displaystyle 3 \times \frac{13}{3}=13$
En multipliant par $7$ on arrive à :
$\displaystyle 7\times 3 \times \frac{13}{3}=7 \times 13$
$\displaystyle 3 \times 7 \times \frac{13}{3}=91$ par commutativité
Comme $\displaystyle 3 \times \frac{91}{3}=91$ on en déduit que
$\displaystyle 7 \times \frac{13}{3}=\frac{91}{3}$
De même $\displaystyle 3 \times \frac{7}{3}=7$
En multipliant par $13$ on arrive à :
$\displaystyle 13 \times 3 \times \frac{7}{3}=13 \times 7$
$\displaystyle 3 \times 13 \times \frac{7}{3}=91$ par commutativité
De même on arrive ainsi à :
$\displaystyle 13 \times \frac{7}{3}=\frac{91}{3}$
Finalement
$\displaystyle 7 \times \frac{13}{3}=\frac{7 \times 13}{3}=13 \times \frac{7}{3}$
Ainsi calculer les 7 tiers de 13 revient bien à multiplier 13 par $\displaystyle \frac{7}{3}$
Sur cet exemple générique nous venons d’établir :
Propriété
$a$, $b$ et $c$ des entiers relatifs avec $b\neq 0$
Calculer la fraction $\displaystyle \frac{a}{b}$ de $c$ revient à effectuer $\displaystyle c \times \frac{a}{b}$
De plus :
$\displaystyle c \times \frac{a}{b}=\frac{a \times c}{b}$
L’égalité des fractions et les fractions irréductibles
Prenons un exemple générique : $\displaystyle \frac{3}{7}$ vérifie $\displaystyle 7 \times \frac{3}{7}=3$
Nous pouvons multiplier cette égalité par $2$ :
$\displaystyle 2 \times 7 \times \frac{3}{7}=2\times 3$
$\displaystyle 14 \times \frac{3}{7}=6$
Or $\displaystyle 14 \times \frac{6}{14}=6$
Il s’en suit par unicité que $\displaystyle \frac{3}{7}=\frac{6}{14}=\frac{3 \times 2}{7 \times 2}$
Propriété
$a$, $b$ et $k$ des nombres entiers relatifs avec $b \neq 0$ et $k \neq 0$
$\displaystyle \frac{a \times k}{b \times b}=\frac{a}{b}$
Remarques :
Un même nombre rationnel peut donc s’exprimer sous la forme d’une infinité de fractions. Cela est très utile pour effectuer des sommes de fractions et écrire des fractions avec un dénominateur commun comme on le verra ci-dessous.
Parmi toutes les fractions égales entre elles, il en existe une qui est la plus simple au sens où les deux nombres entiers considérés ne possèdent aucun diviseurs commun en dehors de 1, on dit dans ce cas que les numérateurs et dénominateurs sont premiers entre eux et que la fraction est irréductible.
L’égalité des fractions et l’égalité des produits en croix
Nous allons montrer l’équivalence entre l’égalité des fractions et l’égalité des produits en croix. Partons à nouveau sur un exemple générique.
Si des fractions sont égales alors les produits en croix sont égaux
Les fractions $\displaystyle \frac{5}{7}$ et $\displaystyle \frac{30}{42}$ sont égales puisque $\displaystyle \frac{30}{42}=\frac{6 \times 5}{6 \times 7}$.
$5 \times 42=5 \times 6 \times 7$
$7 \times 30=7 \times 6 \times 5$
Par commutativité des la multiplication nous en déduisons que si les fractions égales alors les produits en croix sont égaux.
Si les produits en croix sont égaux alors les fractions sont égales
On constate que $5 \times 42=210$ et que $7 \times 30=210$
Ainsi $5 \times 42=7 \times 30$
$\displaystyle \frac{5}{7}=\frac{5 \times 30}{7 \times 30}=\frac{150}{210}$
$\displaystyle \frac{30}{42}=\frac{30 \times 5}{42 \times 5}=\frac{150}{210}$
Les fractions sont donc bien égales entre elles.
Nous venons donc de montrer sur cet exemple générique :
Propriété
Deux fractions sont égales à la seule et unique condition (si et seulement si) leurs produits en croix sont égaux.
$a$, $b$, $c$ et $d$ des entiers relatifs avec $b\neq 0$ et $d\neq 0$
$\displaystyle \frac{a}{b}=\frac{c}{d} si et seulement si a \times d=b \times c$
Sommes algébriques des fractions
On souhaite ajouter les fractions $\displaystyle \frac{5}{7}$ et $\displaystyle \frac{8}{7}$.
On sait que $\displaystyle 7 \times \frac{5}{7}=5$ et que $\displaystyle 7 \times \frac{8}{7}=8$
Ajoutons les deux membres des égalités précédentes :
$\displaystyle 7 \times \frac{5}{7}+7 \times \frac{8}{7}=5+8$
On factorise $7$ en utilisant la distributivité :
$\displaystyle 7 \left (\frac{5}{7}+\frac{8}{7} \right)=13$
Or on sait que $\displaystyle 7 \times \frac{13}{7}=13$
Par définition on en déduit que $\displaystyle \frac{5}{7}+\frac{8}{7}=\frac{13}{7}$
Propriété
$a$, $b$ et $c$ ds nombres entiers relatifs où $c \neq 0$
$\displaystyle \frac{a}{c}+\frac{b}{c}=\frac{a+b}{c}$
Remarque :
Cette propriété est assez faible : elle montre que la somme de fractions est possible à condition que les dénominateurs soient égaux. Cependant l’égalité des fractions permet de mettre en place le moyen de réduire les fractions au même dénominateur.
Écrire deux fractions avec le même dénominateur
Le dénominateur commun à deux fractions est le plus petit multiple commun des deux dénominateurs, dit plus simplement : c’est le plus petit nombre commun que l’on trouve dans les tables de multiplication de ces deux nombres. Une méthode simple consiste à écrire quelques multiples de chacun des nombres jusque trouver un multiple commun, si possible le plus petit. On peut cependant être plus précis :
Si les deux dénominateurs n’ont pas de diviseurs commun, on dit qu’ils sont premiers entre eux, alors le dénominateur commun est le produit des deux nombres. Par exemple :
$\displaystyle \frac{4}{5} + \frac{3}{7}=\frac{4 \times 7}{5 \times 7}+\frac{3\times 5}{7 \times 5}=\frac{28}{35}+\frac{15}{35}=\frac{43}{35}$
Si les deux dénominateurs ont des diviseurs commun, il peut être utile de déterminer le plus grand diviseur commun aux deux nombres. Le plus petit commun multiple est égal au quotient du produit des deux nombres par le plus grand diviseur commun. Par exemple :
$\displaystyle \frac{7}{12}+\frac{11}{15}$
Comme $3$ est le plus grand diviseur commun et que $15\times 12=180$ le dénominateur commun est $180 \div 3=60$
$\displaystyle \frac{7}{12}+\frac{11}{15}=\frac{7\times 5}{12\times 5}+\frac{11\times 4}{15\times 15}=\frac{35}{60}+\frac{44}{60}=\frac{79}{60}$
Ces méthodes ne sont pas enseignées en tant que telles puisque la notion de PPCM et de PGCD ne sont pas aux programmes du collège. Cependant ces remarques peuvent être utiles pour enseigner et construire des exemples adaptés.
Produit des fractions
On utilise à nouveau un exemple générique. On souhaite calculer $\displaystyle \frac{3}{5} \times \frac{7}{11}$
Comme $\displaystyle 5 \times \frac{3}{5}=3$ et que $11 \times \frac{7}{11}=7$
On peut multiplier les membres de ces deux égalités :
$\displaystyle 5 \times \frac{3}{5} \times 11 \times \frac{7}{11}=3 \times 7$
$\displaystyle 5 \times 11 \times \frac{3}{5} \times \frac{7}{11}=21$
$\displaystyle 55 \times \frac{3}{5} \times \frac{7}{11}=21$
Or $\displaystyle 55 \times \frac{21}{55}=21$, on en déduit :
$\displaystyle \frac{3}{5} \times \frac{7}{11}=\frac{21}{55}=\frac{3 \times 7}{5 \times 11}$
Propriété
$a$, $b$, $c$ et $d$ des entiers relatifs avec $b\neq 0$ et $d \neq 0$
$\displaystyle \frac{a}{b} \times \frac{c}{d}=\frac{a \times c}{b \times d}$
Remarque :
Il est important de montrer la nécessité de simplifier un produit avant de l’effectuer.
Quotient des fractions et notion d’inverse
Approche technique par l’égalité des produits en croix
Sur un exemple générique montrons comment effectuer le quotient de $\displaystyle \frac{5}{3}$ par $\displaystyle \frac{8}{7}$.
Par définition d’un quotient ce nombre est celui qui multiplié par $\displaystyle \frac{8}{7}$ est égal à $\displaystyle \frac{5}{3}$
Cette approche est compliqué même en écrivant la question sous forme algébrique et faisant l’hypothèse raisonnable que le quotient cherché est une fraction du type $\displaystyle \frac{a}{b}$ où $b \neq 0$
$\displaystyle \frac{8}{7} \times \frac{a}{b}=\frac{5}{3}$
$\displaystyle \frac{8a}{7b}=\frac{5}{3}$
Une approche par l’égalité des produits en croix permet de résoudre de manière technique cette question :
$3 \times 8a=7b \times 5$
$24a=35b$
Il y a alors un passage délicat, car cette égalité revient à dire (est équivalente à) par les produits en croix :
$\displaystyle \frac{a}{b}=\frac{35}{24}$
Il faut alors remarquer que $\displaystyle \frac{35}{24}=\frac{5\times 7}{8 \times 3}=\frac{5}{3} \times \frac{7}{8}$.
Il est très artificiel de constater que multiplier par $\displaystyle \frac{7}{8}$ revient à diviser par $\displaystyle \frac{8}{7}$!
Cette manière de faire me semble peu convaincante. Voici une seconde manière de voir que je préfère présenter à mes élèves
Notion d’inverse
On reprend un des résultats précédents affirmant que $\displaystyle 13 \times \frac{1}{3}=\frac{13}{3}$
Il signifie exactement que $\displaystyle 13 \div 3=\frac{13}{3}=13 \times \frac{1}{3}$
Donc diviser $13$ par $3$ revient à multiplier $13$ par $\displaystyle \frac{1}{3}$.
De cet exemple générique on en déduit que diviser par un nombre entier relatif non nul $b$ revient à multiplier par la fractions $\displaystyle \frac{1}{b}$
Or par définition $\displaystyle b \times \frac{1}{b}=1$
On arrive ainsi à la définition suivante :
Définition
$b$ un nombre entier relatif non nul l’inverse de $b$ est le nombre $\displaystyle \frac{1}{b}$, il vérifie l’égalité $\displaystyle b \times \frac{1}{b}=1$
On se propose maintenant d’étendre la notion d’inverse aux nombres rationnels.
Repartons d’un exemple générique et cherchons l’inverse de la fraction $\displaystyle \frac{8}{7}$.
L’inverse du nombre $\displaystyle \frac{8}{7}$ serait donc un nombre dont le produit avec $\displaystyle \frac{8}{7}$ est égal à $1$.
Il est simple de constater que $\displaystyle \frac{8}{7} \times \frac{7}{8}=\frac{8 \times 7}{7 \times 8}=1$
Définition
$a$ et $b$ des entiers relatifs avec $b \neq 0$
L’inverse de la fraction $\displaystyle \frac{a}{b}$ est la fraction $\displaystyle \frac{b}{a}$ et on a $\displaystyle \frac{a}{b} \times \frac{b}{a}=1$
Montrons maintenant que diviser par $\displaystyle \frac{8}{7}$ revient bien à multiplier par $\displaystyle \frac{7}{8}$
$\displaystyle \frac{5}{3} \times \frac{7}{8}=\frac{35}{24}$
Vérifions que $\frac{35}{24}$ est bien la réponse attendue :
$\displaystyle \frac{8}{7} \times \frac{35}{24}=\frac{8 \times 35}{7 \times 24}=\frac{8 \times 5 \times 7}{7 \times 8 \times 3}=\frac{5}{3}$
On prouve donc ainsi que $\displaystyle \frac{5}{3} \div \frac{8}{7}=\frac{35}{24}$
Un autre raisonnement consiste à repartir de la question de départ qui consiste à trouver le nombre qui multiplié par $\displaystyle \frac{8}{7}$ est égal à $\displaystyle \frac{5}{3}$. Notons $x$ ce nombre.
$\displaystyle \frac{8}{7} \times x=\frac{5}{3}$
On multiplie cette égalité par $\displaystyle \frac{7}{8}$
$\displaystyle \frac{7}{8} \times \frac{8}{7} \times x =\frac{7}{8} \times \frac{5}{3}$
$\displaystyle 1 \times x=\frac{7}{8} \times \frac{5}{3}$
$\displaystyle x=\frac{35}{24}$
Dans la présentation en classe il n’est pas nécessaire d’utiliser explicitement une équation en $x$ mais sous forme d’égalité à trou !
Finalement quelque soit la méthode on arrive à la propriété générale suivante :
Propriété
$a$, $b$, $c$ et $d$ des entiers naturels avec $b \neq 0$ et $d \neq 0$
$\displaystyle \frac{a}{b} \div \frac{c}{d}=\frac{a}{b} \times \frac{d}{c}$
Remarque
La notation $\displaystyle \frac{\frac{5}{3}}{\frac{8}{7}}=\frac{5}{3} \div \frac{8}{7}$ peut être introduite à ce moment là.
Plus important encore, nous venons de montrer la propriété suivante :
Propriété
Diviser par un nombre non nul revient à multiplier par son inverse.
Remarque
Cela signifie que dorénavant nous considérerons la division comme une multiplication. Nous avions quatre opérations en arrivant au collège, la soustraction est devenue l’addition de l’opposé grâce à l’introduction des nombres relatifs, la division devient la multiplication grâce aux nombres rationnels. Nous voici maintenant avec deux opérations, l’addition et la multiplication, et les symétriques de chaque opération, opposé pour la soustraction, inverse pour la multiplication.
Nous voici donc en présence du corps $\mathbb{Q}$ des nombres rationnels muni des opérations d’addition et de multiplication.
Les repères annuels de progression
Ils indiquent de manière très précises les notions à aborder chaque année et même à chaque période de l’année. Ils seront en vigueur à la rentrée 2019 et font l’objet d’une appropriation durant l’année 2018. C’est une des raisons de cet article !
Voici le lien Eduscol !
Sixième
Nous sommes encore au cycle 3. Voici les repères annuels de progression :
- En période 1, sont réactivées les fractions comme opérateurs de partage vues en CM, puis les fractions décimales en relation avec les nombres décimaux (par exemple à partir de mesures de longueurs) ; les élèves ajoutent des fractions décimales de même dénominateur.
- En période 2 l’addition est étendue à des fractions de même dénominateur (inférieur ou égal à 5 et en privilégiant la vocalisation : deux cinquièmes plus un cinquième égale trois cinquièmes).
- En période 3, les élèves apprennent que b a est le nombre qui, multiplié par b, donne a (définition du quotient de a par b).
Cinquième
Voici les repères annuels de progression pour cette première année du cycle 4 :
- La conception d’une fraction en tant que nombre, déjà abordée en sixième, est consolidée.
- Les élèves sont amenés à reconnaître et à produire des fractions égales (sans privilégier
de méthode en particulier), à comparer, additionner et soustraire des fractions dont les dénominateurs sont égaux ou multiples l’un de l’autre. - Au moins une des propriétés suivantes est démontrée, à partir de la définition d’un quotient :
- $\displaystyle \frac{a \times b}{a\times c}=\frac{b}{c}$
- $\displaystyle a \times \frac{b}{c}=\frac{a \times b}{c}$
- $\displaystyle \frac{a}{b}+\frac{c}{b}=\frac{a+c}{b}$
- $\displaystyle \frac{a}{b}-\frac{c}{b}=\frac{a-c}{b}$
- Il est possible, à ce niveau, de se limiter à des exemples à valeur générique. Cependant, le professeur veille à spécifier que la vérification d’une propriété, même sur plusieurs exemples, n’en constitue pas une démonstration.
Quatrième
Voici les repères annuels de progression pour cette seconde année du cycle 4 :
- Un nombre rationnel est défini comme quotient d’un entier relatif par un entier relatif non nul, ce qui renvoie à la notion de fraction. Le quotient de deux nombres décimaux peut ne pas être un nombre décimal.
- La notion d’inverse est introduite, les opérations entre fractions sont étendues à la multiplication et la division.
- Les élèves sont conduits à comparer des nombres rationnels, à en utiliser différentes représentations et à passer de l’une à l’autre.
- Une ou plusieurs démonstrations de calculs fractionnaires sont présentées. Le recours au calcul littéral vient compléter pour tout ou partie des élèves l’utilisation d’exemples à valeurs génériques.
Troisième
Voici les repères annuels de progression pour la dernière année du cycle 4
- La notion de fraction irréductible est abordée, en lien avec celles de multiple et de diviseur qui sont travaillées tout au long du cycle.
Quelques éléments d’histoire des mathématiques
Les fractions en Mésopotamie
Les mathématiques mésopotamiennes sont les premières traces écrites de mathématiques disponibles en archéologie. Cette période commence au quatrième millénaire avant notre ère vers -3400 et se poursuit jusque la chute de Babylone en -539. De nombreuses tablettes d’argile ont été découvertes au XIX ème siècle, elles attestent des mathématiques de cette époque : système d’écriture des nombres, écriture sexagésimale, opérations arithmétiques… Géographiquement cette civilisation se trouve entre la Syrie, l’Irak et l’Iran actuels.
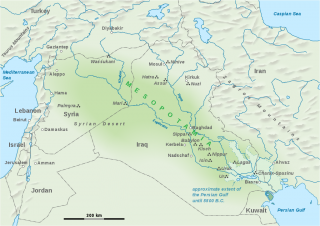
Je n’ai pas la prétention d’écrire ici un article sérieux d’histoire des mathématiques. Voici cependant quelques éléments qui concernent les fractions.
La numération babylonienne utilise une base soixante, une base sexagésimale. C’est une écriture additionnelle constituée de deux symboles : le clou et le chevron.

Le nombre soixante est avantageux, il possède de nombreux diviseurs propres : 2, 3, 4, 5, 6, 10, 12, 15, 20, 30.
Pour diviser les babyloniens utilisait la multiplication par l’inverse $\displaystyle a \div b = a \times \frac{1}{b}$. La division revenait ainsi à une multiplication. On trouve ainsi dans cette civilisation des tables d’inverses, c’est à dire les inverses des nombres entiers écrits en base 60.
Voici une telle table que l’on peut trouver au Louvre :
Voyons comment ces tables pouvaient servir au babyloniens.
En s’inspirant de l’écriture décimale de $\frac{1}{2}=\frac{5}{10}=0,5$ on peut écrire en base soixante
$\displaystyle \frac{1}{2}=\frac{30}{60}=0:30$ (j’utilise le symbole : pour la virgule en sexagésimal.)
$\displaystyle \frac{1}{3}=\frac{20}{60}=0:20$
$\displaystyle \frac{1}{4}=\frac{15}{60}=0:15$
$\displaystyle \frac{1}{5}=\frac{12}{60}=0:12$
$\displaystyle \frac{1}{6}=\frac{10}{60}=0:10$
On voit l’intérêt de la base 60 !
Cela se complique avec l’inverse de 7 et de 8.
Commençons par l’inverse de 8. Il peut être utile de consulter d’abord la méthode générique pour obtenir une approximation décimale d’une fraction en lisant un peu plus bas.
On veut donc l’écriture sexagésimale de la fraction $\displaystyle \frac{1}{8}$
$1\times 1=1=0\times 8+1$
$60\times 1=60=7\times 8+4$
$60\times 4=240=30 \times 8+0$
Ainsi $\displaystyle \frac{1}{8}=0+\frac{7}{60}+\frac{30}{3~600}$
L’écriture sexagésimale de $\displaystyle \frac{1}{8}$ est $0:7:30$
Pour $7$ on a une difficulté : il n’y a pas d’écriture sexagésimale finie de l’inverse de 7.
$60=8\times 7+4$
$60\times 4=240=34 \times 7+2$
$60\times 2=120=17 \times 7+1$
$60 \times 1=60=8\times 7+4$
Une approximation sexagésimale de l’inverse de 7 est donc $0:8:34:17:8:34:17…$
Les babyloniens avaient obtenus de telles approximations que l’on retrouve sur les tablettes archéologiques.
Les fractions en Egypte
En cours de rédaction
Les fractions en Grèce
En cours de rédaction
Les fractions dans les mathématiques arabes
En cours de rédaction
Les fractions aujourd’hui
En cours de rédaction
Quelques prolongements pour les élèves curieux
Fractions et écriture décimale
La calculatrice donne très rapidement une valeur décimale ou approchée pour les fractions. On en oublie le sens de l’écriture décimale. Il peut être intéressant de montrer le lien entre écriture décimale et fraction. Voici quelques pistes :
Propriété
Tout nombre décimal peut s’écrire sous la forme d’une fraction
Sur un exemple générique on peut montrer cette propriété.
Par exemple le nombre décimal $3,141592$ (qui n’est pas égal au nombre $\pi$) peut s’écrire ainsi :
$\displaystyle 3,141592=\frac{3~141~592}{100~000}$
En fait, il s’agit même de la définition d’un nombre décimal : un nombre est décimal si on peut l’écrire sous la forme d’une fractions dont le dénominateur est une puissance de 10 (le numérateur est un entier relatif !). Pour les nombres entiers il faut penser à écrire $\displaystyle 2~018=\frac{2~018}{1}=\frac{2~018}{10^0}$
L’ensemble des nombres décimaux est donc un sous-ensemble de l’ensemble des nombres rationnels (les fractions). C’est même un anneau principal inclus dans le corps des rationnels.
On peut maintenant s’intéresser à l’approximation décimale des fractions. Cela consiste à écrire une fraction sous la forme d’une somme de fractions décimales (dont le dénominateur est une puissance de 10).
Partons de la fraction $displaystyle \frac{17}{8}$
$\displaystyle \frac{17}{8}=\frac{16}{8}+\frac{1}{8}=2+\frac{1}{8}$
$\displaystyle 10 \times \frac{1}{8}=\frac{10}{8}=1+\frac{2}{8}=1+\frac{1}{4}$
Donc $\displaystyle=\frac{1}{8}=\frac{1}{10}+\frac{1}{40}$
$\displaystyle 100 \times \frac{1}{40}=\frac{100}{40}=2+\frac{20}{40}=2+\frac{1}{2}$
Donc $\displaystyle=\frac{1}{40}=\frac{2}{100}+\frac{1}{200}$
$\displaystyle 1~000 \times \frac{1}{200}=\frac{1~000}{200}=5$
Bilan : $\displaystyle \frac{17}{8}=2+\frac{1}{10}+\frac{2}{100}+\frac{5}{1~000}=2,125$
La virgule n’est qu’un codage pratique pour désigner cette égalité !
Cette méthode consiste finalement à utiliser l’algorithme usuelle de la division euclidienne avec la potence.
On aurait pu écrire cela à l’aide d’égalités euclidiennes :
$17=8\times 2+1$
$10\times 1=8\times 1+2$
$10\times 2=8\times 2+4$
$10\times 4=8\times 5$
D’où en observant les quotients l’écriture décimale 2,125.
On peut aussi revenir à cette occasion sur les fractions n’ayant pas d’écriture décimale finie comme $displaystyle \frac{1}{7}$ et montrer que cette écriture est forcément périodique à partir d’un certain rang. Mais on sort de l’objet principal de cet article.
L’addition du cancre
Voici un résultat étonnant :
$\displaystyle \frac{1}{3}+\frac{-4}{6}=\frac{2}{6}+\frac{-4}{6}=-\frac{2}{6}=-\frac{1}{3}$
Or $\displaystyle \frac{1+(-4)}{3+6}=\frac{-3}{9}=-\frac{1}{3}$
On arrive à ce résultat dit « addition du cancre » :
$\displaystyle \frac{1}{3}+\frac{-4}{6}=\frac{1+(-4)}{3+6}$
Pour ceux que cela intéresse, on trouve de nombreux autres exemples :
$\displaystyle \frac{2}{4}+\frac{-9}{3}=\frac{-7}{7}$
$\displaystyle \frac{5}{5}+\frac{-5}{5}=\frac{0}{10}$
$\displaystyle \frac{4}{1}+\frac{-6}{3}=\frac{-2}{4}$
$\displaystyle \frac{1}{2}+\frac{-9}{6}=\frac{-8}{8}$
…
En posant $a$, $b$, $c$ et $d$ des entiers relatifs dont $b \neq 0$ et $d \neq 0$ vérifiant l’égalité, on arrive a :
$\displaystyle \frac{a}{b}+\frac{c}{d}=\frac{a+c}{b+d}$
$\displaystyle \frac{ad}{bd}+\frac{cb}{bd}=\frac{a+c}{b+d}$
$\displaystyle \frac{ad+bc}{bd}=\frac{a+c}{b+d}$
$(ad+bc)(b+d)=bd(a+c)$ produits en croix
$abd+ad^2+b^2c+bdc=abd+bcd$
$ad^2+b^2c=0$
$ad^2=-b^2c$
Cette condition nécessaire et suffisante sur $a$, $b$, $c$ et $d$ permet de construire les exemples ci-dessus.
Pour ceux qui s’interrogent sur cette addition du cancre je vous invite à lire les études très précises sur cette opération qu’on appelle la médiante de deux fractions et possèdent des applications inatendues :
Les fractions continues
Les fractions continues ont été utilisées dès le moyen-âge et restent un domaine vivant des mathématiques.
On peut proposer d’effectuer les calculs suivants :
$\displaystyle 1+\frac{1}}{1}=1+1=2$
$\displaystyle 1+\frac{1}{1+\frac{1}{1}}=1+\frac{1}{2}=\frac{2}{2}+\frac{1}{2}=\frac{3}{2}$
$\displaystyle 1+\frac{1}{1+\frac{1}{1+\frac{1}{1}}}=1+\frac{1}{\frac{3}{2}}=1+\frac{2}{3}=\frac{3}{3}=\frac{2}{3}+\frac{3}{3}=\frac{5}{3}$
$\displaystyle 1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1}}}}=1+\frac{1}{\frac{5}{3}}=1+\frac{3}{5}=\frac{5}{5}+\frac{3}{5}=\frac{8}{5}$
$\displaystyle 1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{1}}}}}=1+\frac{1}{\frac{8}{5}}=1+\frac{5}{8}=\frac{8}{8}+\frac{5}{8}=\frac{13}{8}$
…
On peut ensuite jouer avec la suite de Fibonacci : 1 – 1 – 2 – 3 – 5 – 8 – 13 – 21 – …
Et avec les suites partielles qui tendent vers le nombre d’or !
L’écriture en fraction continue du nombre d’or est donc $\displaystyle \frac{1+\sqrt{5}}=[1;1;1;1;1…]$
Pour mémoire le nombre $\pi= [3;7;15;1;292;1;1;2;1…]$ soit $\displaystyle \pi=3+\frac{1}{7+\frac{1}{15+\frac{1}{1+\frac{1}{292+\frac{1}{…}}}}}}$
Les réduites des fractions continues sont les meilleurs approximations des nombres réels.
Un autre exemple $\sqrt{2}=[1;2;2;2;2;2;2…]$ c’est le cas des nombres réels se calculant à l’aide du racine carrée.
Un autre joli résultat : les nombres rationnels ont écriture finie en fraction continue.
Prenons l’exemple de $\displaystyle \frac{19}{7}$
$\displaystyle \frac{19}{7}=2+\frac{5}{7}=2+\frac{1}{\frac{7}{5}}$
$\displaystyle \frac{7}{5}=1+\frac{2}{5}=1+\frac{1}{\frac{5}{2}}$
$\displaystyle \frac{5}{2}=2+\frac{1}{2}$
Ainsi $\displaystyle \frac{19}{7}=2+\frac{1}{1+\frac{1}{2}}$
On constate que ce processus est fini puisque la suite des numérateurs et dénominateurs est décroissante.
Évidemment, réciproquement, une écriture finie en fraction continue correspond à un nombre rationnel
Voilà de quoi occuper nos petits curieux !















Laisser un commentaire