Tâche complexe quatrième : présentation
Voici une tâche complexe pour la classe de quatrième : la chenille du centre Pompidou.
L’énoncé donné aux élèves est le suivant :
La « chenille » est le nom donné à l’escalier mécanique du Centre Pompidou à Paris accroché à la façade côté du parvis.
Calculer une valeur approchée de la longueur de la « chenille ».

Voilà cet escalier de plus près…

Document élève
Voici le document distribué en classe.

Une proposition de correction
On remarque que la chenille est partagée en 11 portions : 5 portions inclinées, 6 horizontales.
La distance horizontale parcourue sur chaque portion est donc : $latex \frac{180~m}{11} \approx 16,36~m$
La distance verticale parcourue sur chaque portion est donc : $latex \frac{45,5~m}{5}=9,1~m$
Reste à calculer la longueur d’une portion inclinée. On peut schématiser la situation ainsi :
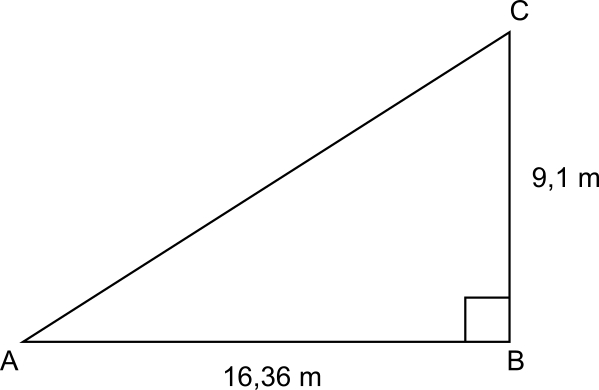
On peut donc utiliser le théorème de Pythagore dans le triangle ABC rectangle en B
$latex BA^2+BC^2=AC^2$
$latex 16,36^2+9,1^2=AC^2$
$latex AC^2=350,4596$
$latex AC=\sqrt{350,4596} \approx 18,72~m$
Reste à calculer une valeur approchée de la longueur de la chenille :
$latex 16,36~m \times 6 + 18,72~m \times 5=191,76~m$
Une valeur approchée de la longueur de la chenille est $latex 191,76~m$















Laisser un commentaire