Les nouveaux programmes du collège applicable en septembre 2016, introduisent un nouveau domaine en mathématiques : Algorithmique et programmation. Entre autre proposition, le jeu de Tic Tac Toe, le fameux morpion à 9 cases ou OXO est proposé par les nouveaux programmes.
Les attendus de fin de cycle sont écrire, mettre au point et exécuter un programme simple. Dans les connaissances et compétences associées ont lit décomposer un problème en sous-problèmes afin de structurer un programme, et en exemple le jeu de tic tac toe.
Viennent ensuite les notions d’algorithme, de variable, de déclenchement d’une action par un événement…
Je vous propose dans cet article d’illustrer ce domaine Algorithmique et programmation à travers le jeu de Tic tac toe. L’objectif étant de programmer un plateau de jeu de Tic Tac Toe en utilisant Scratch, plateau décliné en plusieurs versions de complexité ce qui permet à chaque élève d’atteindre les objectifs des nouveaux programmes suivant ses compétences. Je propose de rassembler ici un maximum d’informations concernant ce jeu, quitte à dépasser le cadre d’un enseignement de collège, l’objectif étant de me fournir et de fournir à mes lecteurs le plus d’éléments pour construire une séquence pédagogique Algorithmique et programmation à l’aide du Tic Tac Toe
Étude sommaire du jeu de Tic tac toe
Le tic tac toe que nos enfants appelle souvent le morpion est un jeu de plateau qui se joue dans une grille carrée 3×3 de 9 cases.
Chaque joueur à son tour marque une case d’un symbole, souvent une croix et un rond. Le premier ayant obtenu un alignement vertical, horizontal ou en diagonale de trois symboles est déclaré vainqueur.
La partie s’achève quand l’un des deux est gagnant ou quand la grille est complète auquel cas les deux joueurs peuvent être à égalité.
Les cases gagnantes
Il y a ainsi 8 alignements gagnants :
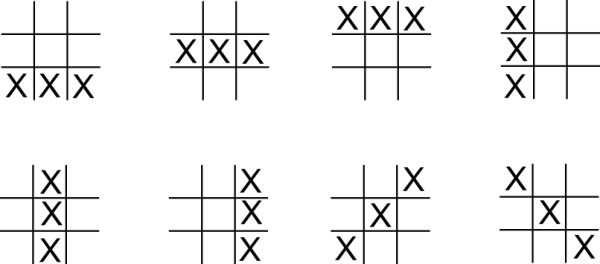
Les cases du plateau ne sont donc pas équitables :

La case centrale est commune à 4 alignements sur 8, soit une fréquence de 50%.
Les quatre cases centrées sont chacune dans 2 alignements sur 8, soit 25%.
Les quatre cases coins sont chacune dans 3 alignements sur 8, soit 36,25%.
Cela nous donne donc un premier ordre de préférence pour cocher ces cases.
Le jeu s’achève bien sur quand les neuf cases sont cochées. Le joueur qui joue le premier va donc jouer 5 fois et le second 4 fois. Comme 9 est impair, le joueur qui commence coche la dernière case.
Une partie maximale compte donc 9 coups. Une partie minimale doit produire un alignement de 3 cases. Si c’est le premier jour qui réussit cet exploit, alors cet alignement arrivera au 5 eme coups. Le premier joueur aura joué 3 fois, le second 2 fois, 4 cases sont vides.
Les symétries du jeu de Tic tac toe
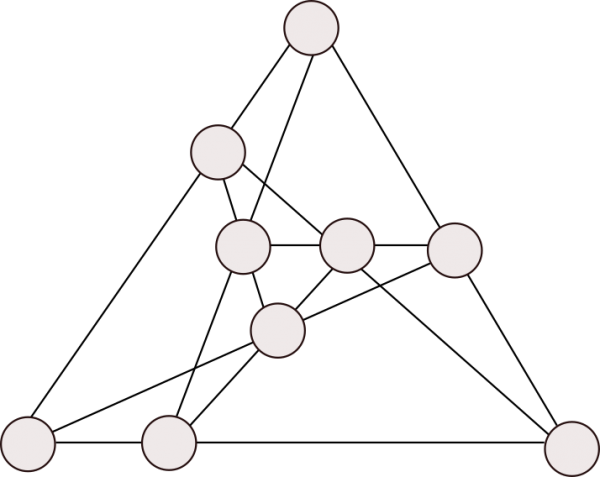
Le plateau de Tic tac toe compte de nombreuses symétries. Une symétrie verticale d’axe central, une symétrie horizontale d’axe central, deux symétrie diagonales d’axe les diagonales. Partons d’une configuration finale et observons l’effet de ces symétries sur cette configuration.
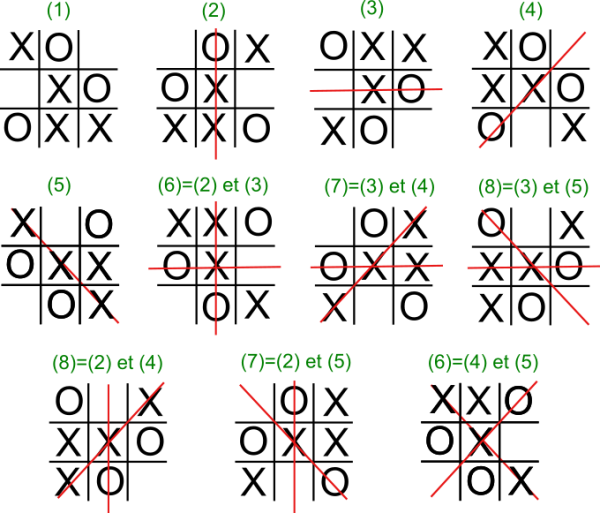
- (1) est la situation finale ;
- (2) la symétrie de (1) par la symétrie d’axe horizontal ;
- (3) la symétrie de (1) par la symétrie d’axe vertical ;
- (4) la symétrie de (1) par la symétrie d’axe première diagonale ;
- (5) la symétrie de (1) par la symétrie d’axe seconde diagonale ;
- (6) on applique (2) puis (3) ;
- (7) on applique (2) puis (4) ;
- (8) on applique (2) puis (5).
On remarque assez vite que (2) puis (3) ou (3) puis (2) donne le même résultat. Ces opérations sont indépendantes de l’ordre, on dit qu’elles sont commutatives. C’est le cas de (4) et (5) aussi. Par contre (2) et (4) ne revient pas à (4) et (2) idem avec (3) et (5) qui ne commutent pas !
On remarque aussi que (2) puis (3) donne la même chose que (4) puis (5) soit un symétrie centrale de centre la case centrale.
On remarque enfin que (2) puis (4) revient à faire (3) et (5) ou que (3) et (4) revient à faire (2) et (5).
Il y a des raisons mathématiques à cela qui dépasse le cadre du collège. Cependant on peut facilement conjecturer que lorsque l’on effectue deux symétries axiales d’axes perpendiculaires ( on dit que l’on compose les symétries ) on obtient un symétrie centrale de centre l’intersection des axes. D’ailleurs c’est une rotation d’angle 180°.
Pour aller plus loin, on connaît le résultat suivant : la composition de deux symétries axiales d’axes sécants est une rotation dont le centre est le point d’intersection et l’angle le double de l’angle formée par les deux droites.
Ainsi on comprend pourquoi (2) puis (4) revient à faire (3) puis (5) ( en maths on écrit plutôt (3) o (5)=(2) o (4)… )
En effet les axes (2) et (4) forment un angle de 45°, ce qui donne une rotation de 90° dans le sens inverse des aiguilles d’une montre. C’est aussi le cas de (3) et (5) !
Les mathématiciens parlent alors d’un groupe non abélien à 8 éléments ! Le groupe des symétries du carré.
Finalement chaque configuration finale peut se décliner de 8 manières symétriques
Nombre de configurations finales possibles
Cette première analyse permet de se demander combien de parties sont possibles au Tic Tac Toe. Dans un premier temps nous pourrions compter ces parties en observant la grille finale.
… ( à compléter )
Comment gagner ou ne pas perdre au Tic Tac Toe ?
Comme on vient de le voir, il y a trois types de cases dans ce jeu :
- la case centrale, qui permet de gagner sur 4 lignes ;
- les cases coins qui permettent de gagner sur chacune 3 lignes ;
- les cases centrées qui permettent de gagner sur 2 lignes.
Le joueur 1 qui commence a donc un avantage en jouant le centre du plateau.
 Le joueur 2 a alors deux possibilités symétriques : une case coin ou une case centrée.
Le joueur 2 a alors deux possibilités symétriques : une case coin ou une case centrée.

Dans le second cas, le joueur 1 domine le jeu, met le joueur 2 sur la défensive et gagne en ouvrant deux lignes auxquelles le joueurs 2 ne peut résister.
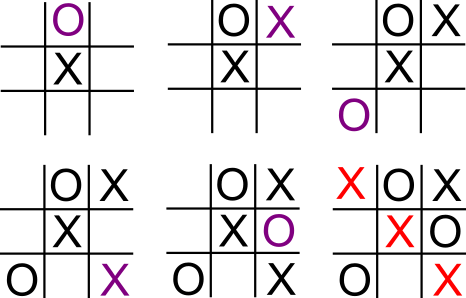
Dans le premier cas, le joueur 1 doit jouer dans la même diagonale que le joueur 2 :
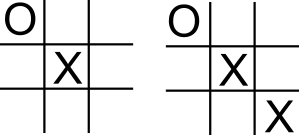
Le joueur 2 doit alors jouer sur la même ligne que la ligne de départ pour ne pas perdre, le joueur 1 sera alors sur la défensive et le joueur 2 obtient un match nul.
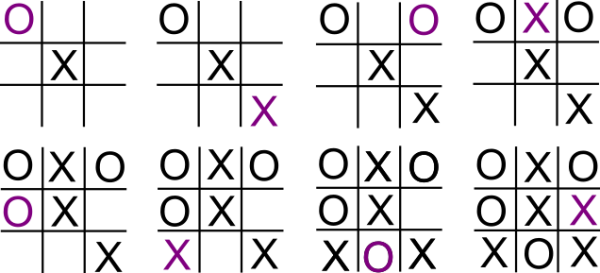
Si le joueur 2 ne joue pas sur la ligne de départ, il perd dans tous les cas.
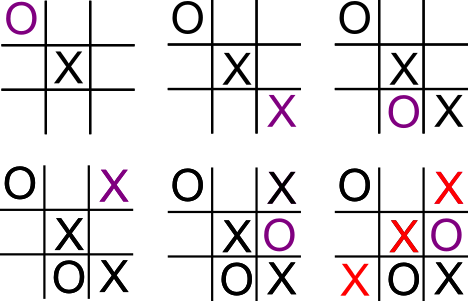
On constate donc que le joueur 1, en jouant parfaitement, gagne ou au pire ne perd pas. Il y a une vraie dissymétrie dans le jeu qui favorise le premier joueur
Une version de Martin Gardner
Pour supprimer cette dissymétrie de départ, le mathématicien Martin Gardner, spécialiste des jeux a proposé un plateau de départ différent. Celui-ci permet à chaque joueur d’être a égalité dès le premier coup : l’avantage à jouer le premier disparaît sur ce plateau.
Je vous propose de faire une petite partie sur Scratch pour tester !
Tic Tac Toe et carré magique
J’ai également découvert sur le serveur de l’IREM de Grenoble un document faisant le lien entre le carré magique classique à 9 cases et le Tic Tac Toe. Cela permet une variante un peu plus difficile, surtout si on ne connaît pas les carrés magiques. Ce document propose aussi d’autres variantes, dont une avec des mots dans chaque case où il faut cocher des mots ayant au moins une lettre en commun !
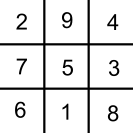
C’est le seul carré magique 3×3. Chaque ligne, chaque colonne et chaque diagonale à une somme de 15.
Jouer sur cette grille revient au Tic Tac Toe classique.
On peut aussi compliquer le jeu en réordonnant les nombres. Le premier ayant coché une somme de 15 est vainqueur. On appelle ce jeu, le jeu de 15.
Enfin voici une dernière version proposée par l’IREM de Grenoble avec des mots :
Voici 9 mots :
- HONTE
- TANTE
- TIGE
- OR
- ARCHE
- IRIS
- OUEST
- SALE
- HISTOIRE
Il faut cocher les mots l’un après l’autre. Le premier qui coche trois mots ayant une lettre commune est gagnant. Il suffit de placer ces mots dans une grille de Tic Tac Toe pour comprendre.
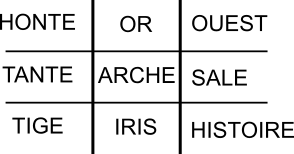
Modélisation du plateau du Tic Tac Toe
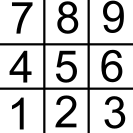
On va numéroter les cases du plateau de cette manière. De bas en haut, de la gauche vers la droite.
Nous allons faire apparaître un symbole dans chaque case. Nous allons modéliser ce symbole en utilisant les nombres suivants :
- 1 pour désigner une case avec un symbole ;
- -1 pour désigner une case avec l’autre symbole ;
- 0 pour une case vide.
Pour gagner le jeux il faut aligner les trois même symboles sur une des 8 lignes possibles.
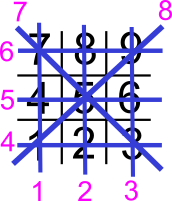
On numérote les 8 lignes comme indiquées ci-dessus.
Sur chacune de ces lignes se trouve donc les valeurs 0, -1 ou 1.
Effectuons toutes les sommes possibles :
- 0+0+0=0
- 0+0+1=1
- 0+0+(-1)=-1
- 0+1+1=2
- 0+(-1)+(-1)=-2
- 0+1+(-1)=0
- 1+1+1=3
- (-1)+(-1)+(-1)=-3
- 1+(-1)+1=1
- 1+(-1)+(-1)=-1
Il y a donc 10 cas possibles sans tenir compte de l’ordre, 10 cas donnant 7 sommes différentes -3, -2, -1, 0, 1, 2 et 3.
Les valeurs 3 et -3 repèrent les situations gagnantes.
Les valeurs 2 et -2 une situation d’alignement de 2 symboles et d’une case vide.
Algorithmique et programmation avec Scratch
Pour une petite présentation de Scratch voici un autre excellent article de ce blog.
Exercice n°1 : mise en place du fond d’écran et des lutins
Objectifs :
- découvrir comment créer un fond d’écran ;
- découvrir les costumes des lutins ;
- faire un premier programme interactif.
Scratch offre un écran de 480×360 pour positionner les lutins. il est repéré en coordonnées cartésiennes sur un axe centré sur le page de -240 à 240 sur l’axe des abscisses et -180 à 180 sur les ordonnées.
On crée un fond d’écran au format vectoriel qui représente la grille. J’ai utilisé l’éditeur vectoriel de Scratch.
Il y a 9 cases à compléter. Nous allons créer 9 lutins et jouer avec les costumes. Je commence par récupérer des images de Stretch et Jessie sur le net pour créer un lutin ayant trois costumes : un blanc, un Stretch, un jessie.
Je commence par le blanc, c’est un rectangle qui fait la taille de mes cases. Je l’utilise ensuite pour créer les costumes Jessie et Strech à la bonne taille.
Four finir avec cet exercice, je décide que cliquer sur la case fait passer le lutin du costume blanc, à Jessie puis Stretch.
Idée importante pour la suite, comme le code d’un lutin devra être copié sur les 8 autres, il vaut mieux peaufiner cette partie avant de copier/coller…
Et voilà le résultat…
Pour reprendre des éléments de projets, utilisez votre compte Scratch et cliquez sur ce lien.
Voici le code, celui du fond d’écran et celui d’un des neuf lutins.
 |
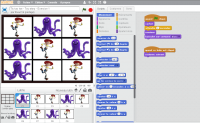 |
Exercice n°2 : chacun son tour on remplit les cases
Objectifs :
- utiliser des variables ;
- choisir au hasard un nombre pour déterminer qui commence ;
- faire un test sur une valeur de variable.
Nous allons maintenant choisir le symbole du joueur de départ. On crée une variable Jessie qui prend les valeurs 0 ou 1 suivant que Jessie ou Stretch doit apparaître.
On crée ensuite 9 variables C1, C2 … C9 ( C comme case ) pour savoir ce que contiennent les cases. 0 pour les cases vides, 1 pour les cases contenant Jessie et -1 pour celle contenant Stretch.
Pour chaque Lutin, on crée l’événement Quand ce lutin est cliqué, puis on teste la valeur de la case qui doit être à 0 pour faire apparaître Jessie ou Stretch.
Pour reprendre des éléments de projets, utilisez votre compte Scratch et cliquez sur ce lien.
Voici le code, celui du fond d’écran et celui d’un des neuf lutins.
 |
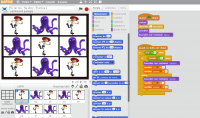 |
Exercice n°3 : utilisation de listes pour améliorer l’application
Objectifs :
- utiliser des listes ;
- garder la mémoire des coups joués ;
- simplifier le code des lutins.
Nous allons utiliser des listes pour améliorer le code de notre application. En particulier nous allons nous débrouiller pour que le code contenu dans chaque lutin soit le plus simple possible.
La liste Case_contenu est initiée avec 9 valeurs 0 pour indiquer que le plateau est vide. Elles passeront à 1 ou -1 en fonction de qui joue.
Un lutin ne doit pas faire grand chose : passer au costume blanc au démarrage et passer au bon costume quand on lui demande. Le reste du code va aller ailleurs !
On utilise deux nouvelles variables : Lutin qui contient le numéro de la case cliquée, Jessie qui contient 1 ou -1 pour coder les costumes, 1 pour Jessie et -1 pour Stretch.
Nous allons utiliser la notion de message entre lutin qui permet de gérer des événements et faire communiquer les éléments du programme. Quand une case est cliquée, elle envoie Clique à tout le monde, la variable Lutin contient son numéro. Chaque Lutin attend le message Apparaît où il teste l’état de la table des cases jouées.
Le programme principal reçoit Clique, le numéro du Lutin et coche la case cliquée avec 1 ou -1 avant d’envoyer le message Apparaît aux lutins.
Pour reprendre des éléments de projets, utilisez votre compte Scratch et cliquez sur ce lien.
Voici le code, celui du fond d’écran et celui d’un des neuf lutins.
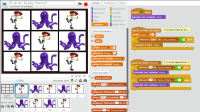 |
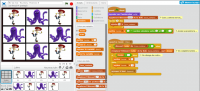 |
Exercice n°4 : fixer les coordonnées des lutins
Objectifs :
- placer les lutins au bon endroit ;
- lire les coordonnées des lutins.
Les lutins peuvent être déplacé. Nous allons fixer leurs coordonnées. Dans Scratch, le plan est rapporté à un repère orthogonal de 480×360. Le centre du repère est placé au centre de la page, nous avons donc des coordonnées allant de -240 à 240 en abscisse et de -180 à 180 en ordonnée.
Nous fixons ces coordonnées pour les lutins en lisant les positions.
Pour reprendre des éléments de projets, utilisez votre compte Scratch et cliquez sur ce lien.
Voici le code, celui du fond d’écran et celui d’un des neuf lutins.
 |
 |
Exercice n°5 : vérifier les victoires et les match nuls
Objectifs :
- analyser le plateau de jeu ;
- déterminer le vainqueur ;
- déterminer les parties nulles ;
- afficher le résultat.
On souhaite aussi faire clignoter les lutins quand une ligne est réalisée et signaler qui a gagné la partie.
On crée deux nouveaux signaux et un tableau :
- Le tableau Ligne est mit à 0 au départ. Il prend la valeur 1 dans une de ses 8 cases quand une des 8 lignes est complète. On numérote les lignes comme dans le dessin.
- Teste victoire : il permet de tester le plateau pour vérifier la présence d’une ligne complète. Pour cela nous faisons 8 tests sur chacune des 8 sommes possibles. Si la ligne est complète elle vaut 3 ou -3. On teste donc la valeur absolue, la fonction abs, qui permet de tester que la valeur 3. On stocke la valeur 1 dans la table ligne.
- Le signal Clignote est envoyé à tous les lutins. Chaque Lutin teste les 2, 3 ou 4 lignes où il apparaît et se met à clignoter.
On ajoute un Lutin qui affiche Victoire de l’un ou l’autre ou partie nulle. Il a 3 costumes. Il teste la présence de 1 dans la table Ligne pour repérer un vainqueur. Il teste ensuite quand le tableau Case_contenu ne contient plus de 0, c’est à dire quand toutes les cases ont été jouées.
À partir de maintenant, l’affichage des lutins est terminé. Tous est prévu, affichage, clignotement. Nous allons pouvoir passer à l’étude d’une mini intelligence artificielle pour faire jouer l’ordinateur contre le joueur.
Le code devient plus important. Je vous renvoie au lien du projet pour le consulter directement sur le site de Scratch.
Exercice n°6 : une première intelligence artificielle : l’ordinateur joue au hasard
Objectifs :
- jouer contre l’ordinateur ;
- l’ordinateur joue au hasard.
On est loin du jeu de Go. On va jouer contre l’ordinateur. Ce dernier jouera au hasard et ne sera donc pas très compétent.
Un nouveau signal est crée, Ordinateur, qui signale que c’est à l’ordinateur de jouer.
Il suffit ensuite de joueur au hasard un nombre entre 1 et 9, pourvu que la case soit libre, l’ordinateur joue en remplissant le tableau Case_contenu.
Bientôt un exercice 7 avec une intelligence un peu plus…. intelligente !















Laisser un commentaire