Le blog de Fabrice ARNAUD

Après ma découverte des flexagones il y a quelques temps, voici le cube de Yoshimoto dont  vous pouvez voir une description ici, une petite merveille mathématiques qu’il est assez facile de construire soi même en papier, vous trouverez le patron un peu plus bas sur cette page.

Ce cube exceptionnel est assez difficile à trouver sur internet. Amazon par exemple me le propose à un tarif incroyable… Vous n’êtes pas obligé de céder à la tentation…

Si comme moi vous préférez utiliser votre argent autrement, voici comment le construire en papier. C’est assez facile, un peu fastidieux tout seul, mais cela peut faire un joli projet de groupe pour des jeunes collégiens.

Je me suis inspiré de cette vidéo japonaise totalement barrée pour construire mon propre Yoshimoto cube.

Le patron de chacun des 16 polyèdres est assez simple, même si il est peu mathématiquement documenté sur cette vidéo. On y voit 3 carrés de 4 cm de côté et 5 triangle isocèle de 2,8 cm de hauteur. Le lien entre la hauteur du triangle isocèle et le côté du carré n’est pas explicité.

Une fois le solide construit, on comprend que les triangles isocèles se rencontrent en un sommet qui est le centre du cube. En effet les six triangles isocèles forment trois des grandes diagonales du cube.

Si on note $latex a$ le côté d’un cube, le théorème de Pythagore nous donne $latex a\sqrt{2}$ pour la diagonale d’un carré puis $latex a\sqrt{3}$ pour la diagonale du cube. Les deux côtés égaux du triangle isocèle mesure donc chacun $latex \dfrac{a\sqrt{3}}{2}$. Si on calcule la hauteur de ce triangle on trouve bien sur $latex \dfrac{\sqrt{2}}{2}a$

Cela confirme notre 2,8 puisque $latex \dfrac{\sqrt{2}}{2} \times 4 \approx 2,83$

Voici enfin un exemple de tel patron à recopier sur papier blanc :

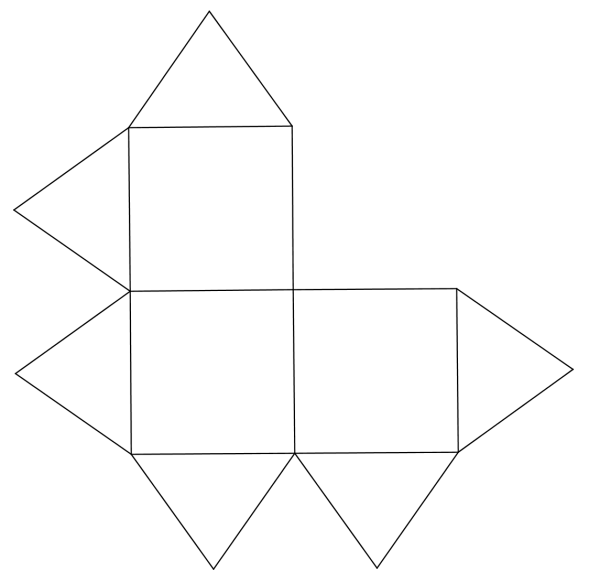
Le cube de Yoshimoto a été découvert en 1971 par Naoki Yoshimoto un mathématicien japonais. Il part d’un dodécaèdre rhombique étoilé pour construire ce fameux cube.

Voici en attendant quelques ressources vidéos supplémentaires qui certainement vous inspirerons :

D’ailleurs, cette géniale vidéo en stop motion se trouve sur le Math Munch où d’autres patrons plus complexes mais amusants sont proposés.